Biết \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right) = \frac{{\sin x}}{{1 + 3\cos x}}\) và \(F\left( {\frac{\pi }{2}} \right) = 2.\) Tính \(F\left( 0 \right).\)
A. \(F\left( 0 \right) = - \frac{1}{3}\ln 2 + 2.\)
B. \(F\left( 0 \right) = - \frac{2}{3}\ln 2 + 2.\)
Quảng cáo
Trả lời:
Cách 1: Ta có \[F\left( x \right) = \int {\frac{{\sin xdx}}{{1 + 3\cos x}}} = - \int {\frac{{d\left( {\cos x} \right)}}{{3\cos x + 1}}} = - \frac{1}{3}\ln \left| {3\cos x + 1} \right| + C.\]
Mà \(F\left( {\frac{\pi }{2}} \right) = - \frac{1}{3}\ln \left| {3\cos \left( {\frac{\pi }{2}} \right) + 1} \right| + C = 2 \Rightarrow C = 2.\)
Do đó, \(F\left( 0 \right) = - \frac{1}{3}\ln \left| {3\cos \left( 0 \right) + 1} \right| + 2 = - \frac{1}{3}\ln 4 + 2 = - \frac{2}{3}\ln 2 + 2.\)
Vậy \(F\left( 0 \right) = - \frac{2}{3}\ln 2 + 2.\)
Cách 2: Sử dụng máy tính cầm tay:
\(\int\limits_0^{\frac{\pi }{2}} {f\left( x \right)} \,{\rm{d}}x = F\left( {\frac{\pi }{2}} \right) - F(0) \Rightarrow F(0) = F\left( {\frac{\pi }{2}} \right) - \int\limits_0^{\frac{\pi }{2}} {\frac{{\sin x}}{{1 + 3\cos x}}} \;{\rm{d}}x.\) Chọn B.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
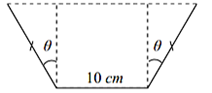
Gọi chiều cao máng nước là: \(h = 10 \cdot \cos \theta \,\,({\rm{cm}})\).
Chiều dài đáy trên máng nước là:
\(10 + 2 \cdot \sqrt {{{10}^2} - {h^2}} = 10 + 2 \cdot \sqrt {{{10}^2} - {{\left( {10 \cdot \cos \theta } \right)}^2}} = 10 + 20 \cdot \sin \theta \,\,({\rm{cm}})\).
Máng nước chứa được nhiều nước nhất khi diện tích hình vẽ lớn nhất
\( \Leftrightarrow S = \frac{{10 + 20 \cdot \sin \theta + 10}}{2} \cdot 10 \cdot \cos \theta = 100 \cdot (1 + \sin \theta ) \cdot \cos \theta = 100 \cdot \left( {\cos \theta + \frac{{\sin 2\theta }}{2}} \right)\).
Ta có \(S' = 100\left( { - \sin \theta + \cos 2\theta } \right) = 100\left( { - \sin \theta + 1 - 2{{\sin }^2}\theta } \right)\)
Khi đó \(S' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\sin \theta = - 1}\\{\sin \theta = \frac{1}{2}}\end{array}} \right.\).
Ta có bảng biến thiên:
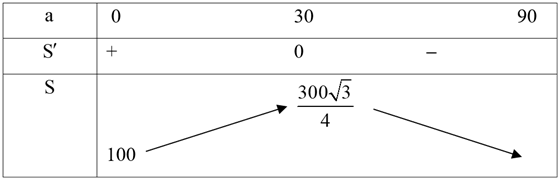
Do đó \({S_{\max }} \Leftrightarrow \sin \theta = \frac{1}{2} \Leftrightarrow \sin \theta = 30^\circ {\rm{.}}\) Đáp án: 30.
Lời giải
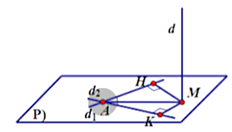
Ta có: \(\overrightarrow {{n_P}} = \left( {1\,;\,\,0\,;\,\, - 1} \right),\,\,\overrightarrow {{u_d}} = \left( { - 1\,;\,\,0\,;\,\,1} \right)\)
\( \Rightarrow d \bot \left( P \right)\) và \(d \cap (P) = M\left( {0\,;\,\,2\,;\,\, - 1} \right)\)
\( \Rightarrow \overrightarrow {MA} = (2; - 1;2) \Rightarrow MA = 3\)
Gọi \[H,\,\,K\] lần lượt là hình chiếu vuông góc của \(M\) lên \({d_1}\) và \({d_2},\) ta có\(d\left( {{d_1}\,;\,\,d} \right) = d\left( {M\,;\,\,{d_1}} \right) = MH,\,\,\,d\left( {{d_2}\,;\,\,d} \right) = d\left( {M\,;\,\,{d_2}} \right) = MK\)
\( \Rightarrow MH = MK = \sqrt 6 \) \( \Rightarrow \sin \widehat {MAK} = \sin \widehat {MAH} = \frac{{HM}}{{AM}} = \frac{{\sqrt 6 }}{3}\)
\( \Rightarrow \cos \left( {{d_1};\,\,{d_2}} \right) = \left| {\cos \left( {2 \cdot \widehat {MAH}} \right)} \right| = \left| {1 - 2{{\sin }^2}\widehat {MAH}} \right| = \left| {1 - \frac{4}{3}} \right| = \frac{1}{3}.\) Đáp án: \(\frac{1}{3}.\)
Câu 3
A. \(S = 4,8.\)
B. \(S = 3,9.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.