Có bao nhiêu số nguyên \(x\) thỏa mãn \({\log _2}\frac{{{x^2} - 1}}{{81}} < {\log _3}\frac{{{x^2} - 1}}{{16}}\)?
Có bao nhiêu số nguyên \(x\) thỏa mãn \({\log _2}\frac{{{x^2} - 1}}{{81}} < {\log _3}\frac{{{x^2} - 1}}{{16}}\)?
A. 68
B. 73
C. 70
D. 72
Quảng cáo
Trả lời:
Điều kiện: \({x^2} - 1 > 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x > 1}\\{x < - 1}\end{array}} \right..\)
Ta có \({\log _2}\frac{{{x^2} - 1}}{{81}} < {\log _3}\frac{{{x^2} - 1}}{{16}}\)
\( \Leftrightarrow {\log _2}\left( {{x^2} - 1} \right) - {\log _2}81 < {\log _3}\left( {{x^2} - 1} \right) - {\log _3}16\)
\( \Leftrightarrow {\log _2}3 \cdot {\log _3}\left( {{x^2} - 1} \right) - 4{\log _2}3 < {\log _3}\left( {{x^2} - 1} \right) - 4{\log _3}2\)
\( \Leftrightarrow \left( {{{\log }_2}3 - 1} \right){\log _3}\left( {{x^2} - 1} \right) < 4\left( {{{\log }_2}3 - {{\log }_3}2} \right)\)
\( \Leftrightarrow {\log _3}\left( {{x^2} - 1} \right) < \frac{{4\left( {{{\log }_2}3 - {{\log }_3}2} \right)}}{{{{\log }_2}3 - 1}}\)\( \Leftrightarrow {\log _3}\left( {{x^2} - 1} \right) < \frac{{4\left( {\frac{1}{{{{\log }_3}2}} - {{\log }_3}2} \right)}}{{\frac{1}{{{{\log }_3}2}} - 1}}\)
\( \Leftrightarrow {\log _3}\left( {{x^2} - 1} \right) < 4\left( {1 + {{\log }_3}2} \right) \Leftrightarrow {\log _3}\left( {{x^2} - 1} \right) < {\log _3}{6^4}\)
\( \Leftrightarrow 0 < {x^2} - 1 < {6^4} \Leftrightarrow \left[ \begin{array}{l}1 < x < \sqrt {1297} \\ - \sqrt {1297} < x < - 1\end{array} \right.\).
Vì \(x\) là số nguyên nên \[x \in \left\{ { - 36\,;\,\, - 35\,;\,\, \ldots ;\,\, - 2\,;\,\,2\,;\,\, \ldots ;\,\,35\,;\,\,36} \right\}.\]
Vậy có 70 số nguyên \(x\) thỏa mãn yêu cầu bài toán. Chọn C.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có \(F\left( x \right) = \int f \left( x \right){\rm{d}}x = \left\{ {\begin{array}{*{20}{l}}{{x^2} + 2x + {C_1}}&{{\rm{ khi }}x \ge 1}\\{{x^3} + x + {C_2}}&{{\rm{ khi }}x < 1}\end{array}} \right.\).
Theo bài ra, ta có \(F\left( 0 \right) = 2 \Rightarrow {C_2} = 2\).
Hàm số \(F\left( x \right)\) liên tục nên \(\mathop {\lim }\limits_{x \to {1^ + }} F\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} F\left( x \right)\)
\[ \Leftrightarrow 3 + {C_1} = 4 \Leftrightarrow {C_1} = 1 \Rightarrow F\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{{x^2} + 2x + 1{\rm{ khi }}x \ge 1}\\{{x^3} + x + 2{\rm{ }}\,\,{\rm{khi }}x < 1}\end{array}} \right.\].
Vậy \(F\left( { - 1} \right) + 2F\left( 2 \right) = {\left( { - 1} \right)^3} + \left( { - 1} \right) + 2 + 2 \cdot \left( {{2^2} + 2 \cdot 2 + 1} \right) = 18.\)
Đáp án: 18.
Câu 2
Lời giải
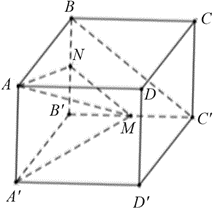
Giả sử cạnh của hình lập phương là \(a > 0.\)
Gọi \(N\) là trung điểm đoạn thẳng \(BB'.\)
Khi đó, \(MN\,{\rm{//}}\,BC'\) nên \(\left( {\widehat {AM\,;\,\,BC'}} \right) = (\widehat {AM\,;\,MN}).\)
Xét \(\Delta A'B'M\) vuông tại \(B'\), ta có
\(A'M = \sqrt {A'{{B'}^{\prime 2}} + B'{M^2}} = \sqrt {{a^2} + \frac{{{a^2}}}{4}} = \frac{{a\sqrt 5 }}{2}.\)Xét \(\Delta AA'M\) vuông tại \(A'\), ta có \(AM = \sqrt {A{{A'}^2} + A'{M^2}} = \sqrt {{a^2} + \frac{{5{a^2}}}{4}} = \frac{{3a}}{2}.\)
Có \[AN = A'M = \frac{{a\sqrt 5 }}{2}\,;\,\,MN = \frac{{BC'}}{2} = \frac{{a\sqrt 2 }}{2}.\]
Trong tam giác \[AMN\] ta có
\(\cos \widehat {AMN} = \frac{{M{A^2} + M{N^2} - A{N^2}}}{{2MA \cdot MN}} = \frac{{\frac{{9{a^2}}}{4} + \frac{{2{a^2}}}{4} - \frac{{5{a^2}}}{4}}}{{2 \cdot \frac{{3a}}{2} \cdot \frac{{a\sqrt 2 }}{2}}} = \frac{{6{a^2}}}{4} \cdot \frac{4}{{6{a^2}\sqrt 2 }} = \frac{1}{{\sqrt 2 }}.\)
Suy ra \(\widehat {AMN} = 45^\circ .\) Vậy \[\left( {AM,\,\,BC'} \right) = \left( {AM,\,\,MN} \right) = \widehat {AMN} = 45^\circ .\] Chọn A.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Gly-Phe-Gly-Ala-Val
B. Gly-Ala-Val-Val-Phe.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.