Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 13)
280 người thi tuần này 4.6 4.5 K lượt thi 150 câu hỏi 150 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 45)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 44)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 43)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 42)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 41)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 40)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 39)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 38)
Danh sách câu hỏi:
Câu 1
PHẦN 1: TƯ DUY ĐỊNH LƯỢNG
Lĩnh vực: Toán học (50 câu – 75 phút)
Câu 1. Một nhóm học sinh lớp 10 trả lời một cuộc khảo sát về khoá học toán mà họ đang theo học. Dữ liệu khảo sát được chia nhỏ như trong bảng sau:
|
|
Môn học |
Tổng |
|||
|
Đại số I |
Hình học |
Đại số II |
|||
|
Giới tính |
Nữ |
35 |
53 |
62 |
150 |
|
Nam |
44 |
59 |
57 |
160 |
|
|
Tổng cộng |
79 |
112 |
119 |
310 |
|
Đáp án nào dưới đây chiếm khoảng 19% tổng số người trả lời khảo sát?
A. Học sinh nữ học Hình học.
B. Học sinh nữ học Đại số II.
Lời giải
Câu 2
Lời giải
Với \(A\left( {{x_0}\,;\,\,{y_0}\,;\,\,{z_0}} \right) \in \left( {Oxyz} \right)\).
Khi đó \(d\left( {A,\,\,\left( {Oxy} \right)} \right) = {z_0}\,,\,\,d\left( {A,\,\,\left( {Oxz} \right)} \right) = {y_0}\,,\,\,d\left( {A,\,\,\left( {Oyz} \right)} \right) = {x_0}.\)
Theo bài ra ta có: \(a = d\left( {M,\,\,\left( {Oxy} \right)} \right) = 2\,;\,\,b = d\left( {M,\,\,\left( {Oyz} \right)} \right) = 1\,;\,\,c = d\left( {M,\,\,\left( {Oxz} \right)} \right) = 3.\)
Suy ra \(P = a + {b^2} + {c^3} = 2 + {1^2} + {3^3} = 30.\) Chọn C.
Câu 3
Lời giải
Ta đặt \(z = a + bi.\)
\(2z - i \cdot \bar z = 3i \Leftrightarrow 2\left( {a + bi} \right) - i\left( {a - bi} \right) = 3i\)
\( \Leftrightarrow 2a - b + i\left( {2b - a} \right) = 3i \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2a - b = 0}\\{2b - a = 3}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 1}\\{b = 2}\end{array}} \right.} \right.\).
Từ đó ta suy ra: \(\left| z \right| = \sqrt {{a^2} + {b^2}} = \sqrt 5 .\) Chọn A.
Câu 4
Lời giải
Phương trình gia tốc: \(a = s'' = f''\left( t \right) = 2t - 2\,\,\left( {\;{\rm{m}}/{{\rm{s}}^2}} \right)\)
Tại \(t = 2\) thì \(a\left( 2 \right) = 2 \cdot 2 - 2 = 2\,\,\left( {\;{\rm{m}}/{{\rm{s}}^2}} \right)\). Chọn D.
Câu 5
Lời giải
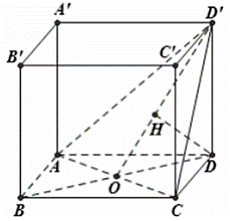
Kẻ \(DH \bot OD'\).
Ta có \[\left\{ \begin{array}{l}AC \bot OD\\AC \bot DD'\end{array} \right. \Rightarrow AC \bot \left( {DOD'} \right) \Rightarrow AC \bot DH\].
Mà \(DH \bot OD'\) nên \(DH \bot \left( {ACD'} \right) \Rightarrow DH = d\left( {D,\,\,\left( {ACD'} \right)} \right)\).
Ta có \(OD = \frac{1}{2}BD = \frac{1}{2}AC = a\) nên
\(\frac{1}{{D{H^2}}} = \frac{1}{{D{{D'}^2}}} + \frac{1}{{O{D^2}}} = \frac{2}{{{a^2}}} \Rightarrow DH = \frac{{a\sqrt 2 }}{2}{\rm{. }}\)Chọn D.Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. \({\left( {x - 4} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 6} \right)^2} = 18.\)
B. \[{\left( {x + 4} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z + 6} \right)^2} = 18.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
A. 68
B. 73
C. 70
D. 72
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 25
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 26
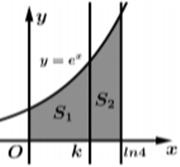
A. \(k = \ln \frac{8}{3}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 29
A. . \(729\pi .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 30
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 32
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 33
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 35
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 51
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 52
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 53
A. lát cắt.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 54
A. chuyển mình.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 55
A. tiến trình.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 56
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 57
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 58
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 59
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 60
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 61
A. so sánh - biểu cảm.
B. nhân hóa - hình tượng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 62
A. Bởi vì/ cho nên.
B. Có lẽ/ bởi vì.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 63
A. nhiệm vụ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 64
A. Thần thoại.
B. Sử thi.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 65
A. đặc biệt.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 66
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 67
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 68
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 69
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 70
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 71
A. Cảnh ngụ tình.
B. Ẩn dụ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 72
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 74
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 75
Đọc đoạn trích sau đây và trả lời câu hỏi:
Thư viết cho em nhòe nét mực
Phên thưa sương muối cứ bay vào
Núi rét đêm qua chừng mất ngủ
Sáng ra thêm bạc một nhành lau.
Ở đây tuyết trắng bên chăn mỏng
Bếp đỏ cơm trưa núi vẫn mờ
Mực đóng thành băng trong ruột bút
Hơ hoài than đỏ chảy thành thư.
(Hữu Thỉnh, Thư mùa đông, https://phunuquandoi.vn)
Chi tiết nào không gợi tả điều kiện khắc nghiệt của thời tiết?
Đọc đoạn trích sau đây và trả lời câu hỏi:
Thư viết cho em nhòe nét mực
Phên thưa sương muối cứ bay vào
Núi rét đêm qua chừng mất ngủ
Sáng ra thêm bạc một nhành lau.
Ở đây tuyết trắng bên chăn mỏng
Bếp đỏ cơm trưa núi vẫn mờ
Mực đóng thành băng trong ruột bút
Hơ hoài than đỏ chảy thành thư.
(Hữu Thỉnh, Thư mùa đông, https://phunuquandoi.vn)
Chi tiết nào không gợi tả điều kiện khắc nghiệt của thời tiết?
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 76
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 77
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 79
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 80
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 81
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 82
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 83
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 84
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 85
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 86
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 87
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 88
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 89
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 90
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 91
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 92
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 93
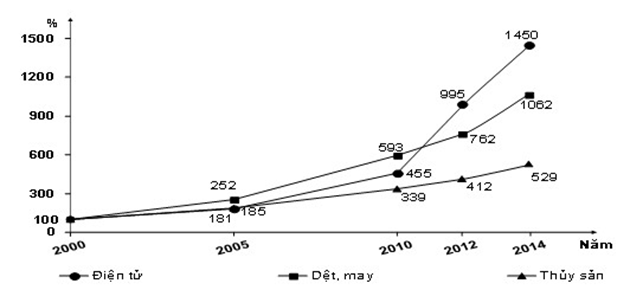
A. Hàng dệt, may có tốc độ tăng trưởng nhanh thứ 2 trong giai đoạn 2012-2014.
B. Nếu tính trong giai đoạn 2000-2010 thì hàng dệt, may đạt tốc độ tăng trưởng cao nhất.
C. Hàng điện tử luôn có tốc độ tăng trưởng cao nhất trong giai đoạn 2000-2014.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 94
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 95
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 96
Vùng Đồng bằng sông Hồng trở thành vùng trọng điểm sản xuất lương thực, thực phẩm của nước ta là do:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 97
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 98
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 99
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 100
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 101
A. \(\frac{3}{2}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 102
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 103
A. 138 ngày.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 105
A. \( \pm 0,034\,\mu m.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 106
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 108
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 110
A. Gly-Phe-Gly-Ala-Val
B. Gly-Ala-Val-Val-Phe.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 111
A. \[5589{\rm{ }}{m^3}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 113
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 114
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 118
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 119
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 120
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 121
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 122
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 123
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 124
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 1
Đọc đoạn trích sau và trả lời các câu hỏi từ 51 đến 55:
Nhớ khi giặc đến giặc lùng
Rừng cây núi đá ta cùng đánh Tây.
Núi giăng thành lũy sắt dày
Rừng che bộ đội, rừng vây quân thù.
Mênh mông bốn mặt sương mù
Đất trời ta cả chiến khu một lòng.
Ai về ai có nhớ không?
Ta về ta nhớ Phủ Thông, đèo Giàng
Nhớ sông Lô, nhớ phố Ràng
Nhớ từ Cao – Lạng, nhớ sang Nhị Hà...
(Việt Bắc – Tố Hữu)
Câu 128
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 129
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 130
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 131
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 132
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 2
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 56 đến 60:
Lần lần, mấy năm qua, mấy năm sau, bố Mị chết. Nhưng Mị cũng không còn tưởng đến Mị có thể ăn lá ngón tự tử nữa. Ở lâu trong cái khổ, Mị quen khổ rồi. Bây giờ thì Mị tưởng mình cũng là con trâu, mình cũng là con ngựa, là con ngựa phải đổi ở cái tàu ngựa nhà này đến ở cái tàu ngựa nhà khác, ngựa chỉ biết việc ăn cỏ, biết đi làm mà thôi. Mị cúi mặt, không nghĩ ngợi nữa, mà lúc nào cũng chỉ nhớ đi nhớ lại những việc giống nhau, tiếp nhau vẽ ra trước mặt, mỗi năm mỗi mùa, mỗi tháng lại làm đi làm lại: Tết xong thì lên núi hái thuốc phiện, giữa năm thì giặt đay, xe đay, đến mùa thì đi nương bẻ bắp, và dù lúc đi hái củi, lúc bung ngô, lúc nào cũng gài một bó đay trong cánh tay để tước thành sợi. Bao giờ cũng thế, suốt năm suốt đời như thế. Con ngựa, con trâu làm còn có lúc, đêm nó còn được đứng gãi chân, đứng nhai cỏ, đàn bà con gái nhà này thì vùi vào việc làm cả đêm cả ngày.
(Vợ chồng A Phủ – Tô Hoài)
Câu 133
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 134
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 135
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 136
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 137
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 61 đến 65:
(1) Tây Tiến đoàn binh không mọc tóc,
(2) Quân xanh màu lá dữ oai hùm.
(3) Mắt trừng gửi mộng qua biên giới,
(4) Đêm mơ Hà Nội dáng kiều thơm.
(5) Rải rác biên cương mồ viễn xứ,
(6) Chiến trường đi chẳng tiếc đời xanh.
(7) Áo bào thay chiếu, anh về đất,
(8) Sông Mã gầm lên khúc độc hành.
(Trích Tây Tiến – Quang Dũng)
Câu 138
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 139
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 140
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 141
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 142
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 66 đến 70:
Khi của cải bắt đầu đến, nó đến nhanh và nhiều đến mức người ta tự hỏi rằng không biết trong những năm tháng gian khó vừa qua nó đã trốn nơi đâu? Phát biểu trên có thể làm bạn kinh ngạc, đặc biệt nếu như bạn luôn suy nghĩ theo quan niệm thông thường rằng sự giàu có chỉ đến với những người làm việc chăm chỉ trong một khoảng thời gian dài. Khi bạn bắt đầu nhận thức được rằng cách nghĩ có thể mang lại sự giàu sang, bạn sẽ thấy rằng sự giàu có luôn bắt nguồn từ một trạng thái mang tính chất tinh thần, từ một mục đích rõ ràng chứ không phải bởi bạn có làm việc cật lực hay không. Những gì mà bạn và mọi người khác nên biết là làm thế nào để có được một trạng thái tinh thần tạo ra sự giàu có như thế. Tôi đã dành hai mươi lăm năm để nghiên cứu điều đó vì bản thân tôi cũng muốn biết “những người giàu có đã làm thế nào để đạt được những thành quả như vậy”. Bạn sẽ nhận thấy rằng ngay khi bạn nắm được những triết lí của nguyên tắc thành công này và bắt đầu ứng dụng những nguyên tắc đó, tình hình tài chính của bạn sẽ được cải thiện. Nói một cách hoa mĩ thì mọi thứ bạn chạm tay vào sẽ biến thành vàng. Bạn cho rằng không thể được ư? Thế mà đúng như vậy đấy.
(Nghĩ giàu làm giàu, Napoleon Hill, NXB Thế giới, 2017)
Câu 143
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 144
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 145
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 146
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 147
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 5
Dựa vào các thông tin sau đây để trả lời các câu hỏi từ câu 108 đến câu 110:
"Nava tập trung mọi cố gắng để xây dựng Điện Biên Phủ thành một tập đoàn cứ điểm mạnh nhất Đông Dương. Tổng số binh lực ở đây lúc cao nhất là 16200 quân, được bố trí thành Ba phân khu: phân khu Bắc gồm các cứ điểm Độc Lập, Bản Kéo; phân khu Trung tâm ở ngay giữa Mường Thanh, nơi đặt sở chỉ huy, có trận địa pháo, kho hậu cần, sân Bay, tập trung 2/3 lực lượng; phân khu Nam đặt tại Hồng Cúm, có trận địa pháo, sân Bay. Tổng cộng cả Ba phân khu có 49 cứ điểm.
Sau khi kiểm tra, các tướng lĩnh Pháp và Mĩ đều coi Điện Biên Phủ là "một pháo đài bất khả xâm phạm". Đầu tháng 12-1953, Bộ Chính trị Trung ương Đảng họp, thông qua kế hoạch tác chiến của Bộ Tổng tư lệnh và quyết định mở chiến dịch Điện Biên Phủ. Mục tiêu của chiến dịch là tiêu diệt lực lượng dịch ở đây, giải phóng vùng Tây Bắc, tạo điều kiện giải phóng Bắc Lào.
Đầu tháng 3-1954, công tác chuẩn bị mọi mặt đã hoàn tất. Ngày 13-3-1954, quân ta nổ súng tấn công tập đoàn cứ điểm Điện Biên Phủ.
Chiến dịch Điện Biên Phủ được chia làm Ba đợt:
Đợt 1, từ ngày 13 đến ngày 17-3-1954: quân ta tiến công tiêu diệt cụm cứ điểm Him Lam và toàn bộ phần khu Bắc Kết quả, ta loại khỏi vòng chiến đấu gần 2000 tên địch.
Đợt 2, từ ngày 30-3 đến ngày 26-4-1954: quân ta đồng loạt tiến công các cứ điểm phía đông phân khu Trung tâm như E1, D1, C1, C2, Al v.v.. Ta chiếm phần lớn các cứ điểm của địch, tạo thêm điều kiện để Bao vây, chia cắt, khống chế địch. Sau đợt này, Mĩ khẩn cấp viện trợ cho Pháp và đe dọa ném bom nguyên tử xuống Điện Biên Phủ. Ta kịp thời khắc phục khó khăn về tiếp tế, nâng cao quyết tâm giành thắng lợi.
Đợt 3 từ ngày 1-5 đến ngày 7-5-1954: quân ta đồng loạt tiến công phân khu Trung tâm và phân khu Nam, lần lượt tiêu diệt các cứ điểm đề kháng còn lại của địch. Chiều 7-5, quân ta đánh vào sở chỉ huy địch. 17 giờ 30 phút ngày 7-5-1954, tướng Đờ Caxtơri cùng toàn bộ Ban Tham mưu của địch đầu hàng và bị bắt sống.
Các chiến trường toàn quốc đã phối hợp chặt chē nhằm phân tán, tiêu hao, kìm chân địch, tạo điều kiện cho Điện Biên Phủ giành thắng lợi".
(Nguồn: SGK Lịch sử 12, NXB Giáo dục Việt Nam, 2023, trang 149-150).
Câu 148
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 149
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 150
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.