Một học sinh làm thí nghiệm đo bước sóng ánh sáng bằng thí nghiệm khe Y-âng. Trong khi tiến hành, học sinh này đo được khoảng cách hai khe sáng là \(1,00 \pm 0,05\left( {mm} \right)\); khoảng cách từ mặt phẳng chứa hai khe đến màn đo được là \(2000 \pm 1,54\left( {mm} \right)\); khoảng cách giữa 10 vân sáng liên tiếp đo được là \(10,80 \pm 0,14\left( {mm} \right)\). Sai số tuyệt đối của quá trình đo bước sóng là

A. \( \pm 0,034\,\mu m.\)

B. \( \pm 0,039\,\mu m.\)

C. \( \pm 0,26\,\mu m.\)

D. \( \pm 0,019\,\mu m.\)

Xem lời giải

Câu hỏi trong đề: Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 13) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Khoảng cách giữa 10 vân sáng liên tiếp là: \(\ell = 9i \Rightarrow \left\{ {\begin{array}{*{20}{l}}{\bar i = \frac{{\overline \ell }}{9} = 1,2{\mkern 1mu} {\mkern 1mu} \left( {mm} \right)}\\{\Delta i = \frac{{\Delta \ell }}{9} = 0,016{\mkern 1mu} {\mkern 1mu} \left( {mm} \right)}\end{array}} \right.\)

Giá trị trung bình của bước sóng là: \(\bar \lambda = \frac{{\bar a.\bar i}}{{\bar D}} = \frac{{{{1.10}^{ - 3}}.1,{{2.10}^{ - 3}}}}{2} = 0,{6.10^{ - 6}}{\mkern 1mu} {\mkern 1mu} \left( m \right) = 0,6{\mkern 1mu} {\mkern 1mu} \left( {\mu m} \right)\)

Sai số tỉ đối của phép đo là: \(\frac{{\Delta \lambda }}{{\bar \lambda }} = \frac{{\Delta a}}{{\bar a}} + \frac{{\Delta i}}{{\bar i}} + \frac{{\Delta D}}{{\bar D}}\)\( \Rightarrow \frac{{\Delta \lambda }}{{0,6}} = \frac{{0,05}}{1} + \frac{{0,016}}{{1,2}} + \frac{{1,54}}{{2000}}\)

\( \Rightarrow \Delta \lambda \approx \pm 0,038{\mkern 1mu} {\mkern 1mu} \left( {\mu m} \right)\). Chọn B.

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{2{\rm{x}} + 2{\rm{ khi x}} \ge 1}\\{3{{\rm{x}}^2} + 1{\rm{ khi }}x < 1}\end{array}} \right..\) Giả sử \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) thoả mãn \(F\left( 0 \right) = 2.\) Giá trị của \(F\left( { - 1} \right) + 2F\left( 2 \right)\) bằng

Xem đáp án

Lời giải

Ta có \(F\left( x \right) = \int f \left( x \right){\rm{d}}x = \left\{ {\begin{array}{*{20}{l}}{{x^2} + 2x + {C_1}}&{{\rm{ khi }}x \ge 1}\\{{x^3} + x + {C_2}}&{{\rm{ khi }}x < 1}\end{array}} \right.\).

Theo bài ra, ta có \(F\left( 0 \right) = 2 \Rightarrow {C_2} = 2\).

Hàm số \(F\left( x \right)\) liên tục nên \(\mathop {\lim }\limits_{x \to {1^ + }} F\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} F\left( x \right)\)

\[ \Leftrightarrow 3 + {C_1} = 4 \Leftrightarrow {C_1} = 1 \Rightarrow F\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{{x^2} + 2x + 1{\rm{ khi }}x \ge 1}\\{{x^3} + x + 2{\rm{ }}\,\,{\rm{khi }}x < 1}\end{array}} \right.\].

Vậy \(F\left( { - 1} \right) + 2F\left( 2 \right) = {\left( { - 1} \right)^3} + \left( { - 1} \right) + 2 + 2 \cdot \left( {{2^2} + 2 \cdot 2 + 1} \right) = 18.\)

Đáp án: 18.

Câu 2

Cho hình lập phương \(ABCD.A'B'C'D'.\) Gọi \(M\) là trung điểm của \(B'C'.\) Góc giữa hai đường thẳng AM và \(BC'\) bằng

A. \(45^\circ .\)

B. \(90^\circ .\)

C. \(30^\circ .\)

D. \(60^\circ .\)

Lời giải

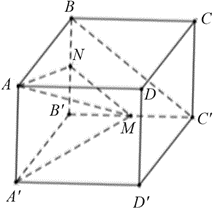
Media VietJack

Giả sử cạnh của hình lập phương là \(a > 0.\)

Gọi \(N\) là trung điểm đoạn thẳng \(BB'.\)

Khi đó, \(MN\,{\rm{//}}\,BC'\) nên \(\left( {\widehat {AM\,;\,\,BC'}} \right) = (\widehat {AM\,;\,MN}).\)

Xét \(\Delta A'B'M\) vuông tại \(B'\), ta có

\(A'M = \sqrt {A'{{B'}^{\prime 2}} + B'{M^2}} = \sqrt {{a^2} + \frac{{{a^2}}}{4}} = \frac{{a\sqrt 5 }}{2}.\)

Xét \(\Delta AA'M\) vuông tại \(A'\), ta có \(AM = \sqrt {A{{A'}^2} + A'{M^2}} = \sqrt {{a^2} + \frac{{5{a^2}}}{4}} = \frac{{3a}}{2}.\)

Có \[AN = A'M = \frac{{a\sqrt 5 }}{2}\,;\,\,MN = \frac{{BC'}}{2} = \frac{{a\sqrt 2 }}{2}.\]

Trong tam giác \[AMN\] ta có

\(\cos \widehat {AMN} = \frac{{M{A^2} + M{N^2} - A{N^2}}}{{2MA \cdot MN}} = \frac{{\frac{{9{a^2}}}{4} + \frac{{2{a^2}}}{4} - \frac{{5{a^2}}}{4}}}{{2 \cdot \frac{{3a}}{2} \cdot \frac{{a\sqrt 2 }}{2}}} = \frac{{6{a^2}}}{4} \cdot \frac{4}{{6{a^2}\sqrt 2 }} = \frac{1}{{\sqrt 2 }}.\)

Suy ra \(\widehat {AMN} = 45^\circ .\) Vậy \[\left( {AM,\,\,BC'} \right) = \left( {AM,\,\,MN} \right) = \widehat {AMN} = 45^\circ .\] Chọn A.

Câu 3