Cho biểu đồ:

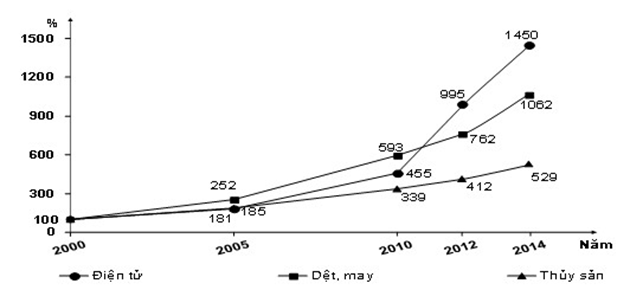
Tốc độ tăng trưởng một số mặt hàng xuất khẩu của Việt Nam

Căn cứ vào biểu đồ đã cho, hãy cho biết nhận xét nào sau đây là không đúng về tốc độ tăng trưởng một số mặt hàng xuất khẩu của Việt Nam?

A. Hàng dệt, may có tốc độ tăng trưởng nhanh thứ 2 trong giai đoạn 2012-2014.

B. Nếu tính trong giai đoạn 2000-2010 thì hàng dệt, may đạt tốc độ tăng trưởng cao nhất.

C. Hàng điện tử luôn có tốc độ tăng trưởng cao nhất trong giai đoạn 2000-2014.

D. Hàng thủy sản có tốc độ tăng chậm hơn so với hai mặt hàng còn lại.

Xem lời giải

Câu hỏi trong đề: Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 13) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Phân tích nội dung các đáp án, ta thấy:

- A đúng: hàng dệt -may có tốc độ tăng trưởng lớn thứ 2 (từ 100% lên 1062%)

- B đúng: giai đoạn 2000-2010 hàng dệt-may có tốc độ tăng trưởng cao nhất (từ 100% lên 593%)

- C không đúng: giai đoạn 2000-2005 hàng điện tử có tốc độ tăng trưởng thấp nhất và năm 2010 tốc độ tăng trưởng đứng thứ 2 → nhận xét tốc độ tăng trưởng hàng điện tử luôn cao nhất trong suốt giai đoạn 2000-2014 là SAI. Chọn C.

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{2{\rm{x}} + 2{\rm{ khi x}} \ge 1}\\{3{{\rm{x}}^2} + 1{\rm{ khi }}x < 1}\end{array}} \right..\) Giả sử \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) thoả mãn \(F\left( 0 \right) = 2.\) Giá trị của \(F\left( { - 1} \right) + 2F\left( 2 \right)\) bằng

Xem đáp án

Lời giải

Ta có \(F\left( x \right) = \int f \left( x \right){\rm{d}}x = \left\{ {\begin{array}{*{20}{l}}{{x^2} + 2x + {C_1}}&{{\rm{ khi }}x \ge 1}\\{{x^3} + x + {C_2}}&{{\rm{ khi }}x < 1}\end{array}} \right.\).

Theo bài ra, ta có \(F\left( 0 \right) = 2 \Rightarrow {C_2} = 2\).

Hàm số \(F\left( x \right)\) liên tục nên \(\mathop {\lim }\limits_{x \to {1^ + }} F\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} F\left( x \right)\)

\[ \Leftrightarrow 3 + {C_1} = 4 \Leftrightarrow {C_1} = 1 \Rightarrow F\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{{x^2} + 2x + 1{\rm{ khi }}x \ge 1}\\{{x^3} + x + 2{\rm{ }}\,\,{\rm{khi }}x < 1}\end{array}} \right.\].

Vậy \(F\left( { - 1} \right) + 2F\left( 2 \right) = {\left( { - 1} \right)^3} + \left( { - 1} \right) + 2 + 2 \cdot \left( {{2^2} + 2 \cdot 2 + 1} \right) = 18.\)

Đáp án: 18.

Câu 2

Cho hình lập phương \(ABCD.A'B'C'D'.\) Gọi \(M\) là trung điểm của \(B'C'.\) Góc giữa hai đường thẳng AM và \(BC'\) bằng

A. \(45^\circ .\)

B. \(90^\circ .\)

C. \(30^\circ .\)

D. \(60^\circ .\)

Lời giải

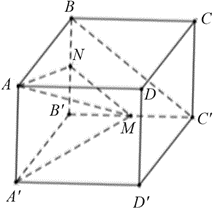
Media VietJack

Giả sử cạnh của hình lập phương là \(a > 0.\)

Gọi \(N\) là trung điểm đoạn thẳng \(BB'.\)

Khi đó, \(MN\,{\rm{//}}\,BC'\) nên \(\left( {\widehat {AM\,;\,\,BC'}} \right) = (\widehat {AM\,;\,MN}).\)

Xét \(\Delta A'B'M\) vuông tại \(B'\), ta có

\(A'M = \sqrt {A'{{B'}^{\prime 2}} + B'{M^2}} = \sqrt {{a^2} + \frac{{{a^2}}}{4}} = \frac{{a\sqrt 5 }}{2}.\)

Xét \(\Delta AA'M\) vuông tại \(A'\), ta có \(AM = \sqrt {A{{A'}^2} + A'{M^2}} = \sqrt {{a^2} + \frac{{5{a^2}}}{4}} = \frac{{3a}}{2}.\)

Có \[AN = A'M = \frac{{a\sqrt 5 }}{2}\,;\,\,MN = \frac{{BC'}}{2} = \frac{{a\sqrt 2 }}{2}.\]

Trong tam giác \[AMN\] ta có

\(\cos \widehat {AMN} = \frac{{M{A^2} + M{N^2} - A{N^2}}}{{2MA \cdot MN}} = \frac{{\frac{{9{a^2}}}{4} + \frac{{2{a^2}}}{4} - \frac{{5{a^2}}}{4}}}{{2 \cdot \frac{{3a}}{2} \cdot \frac{{a\sqrt 2 }}{2}}} = \frac{{6{a^2}}}{4} \cdot \frac{4}{{6{a^2}\sqrt 2 }} = \frac{1}{{\sqrt 2 }}.\)

Suy ra \(\widehat {AMN} = 45^\circ .\) Vậy \[\left( {AM,\,\,BC'} \right) = \left( {AM,\,\,MN} \right) = \widehat {AMN} = 45^\circ .\] Chọn A.

Câu 3