Câu hỏi:

23/07/2024 1,749

Đọc đoạn trích sau đây và trả lời các câu hỏi từ 66 đến 70:

Khi của cải bắt đầu đến, nó đến nhanh và nhiều đến mức người ta tự hỏi rằng không biết trong những năm tháng gian khó vừa qua nó đã trốn nơi đâu? Phát biểu trên có thể làm bạn kinh ngạc, đặc biệt nếu như bạn luôn suy nghĩ theo quan niệm thông thường rằng sự giàu có chỉ đến với những người làm việc chăm chỉ trong một khoảng thời gian dài. Khi bạn bắt đầu nhận thức được rằng cách nghĩ có thể mang lại sự giàu sang, bạn sẽ thấy rằng sự giàu có luôn bắt nguồn từ một trạng thái mang tính chất tinh thần, từ một mục đích rõ ràng chứ không phải bởi bạn có làm việc cật lực hay không. Những gì mà bạn và mọi người khác nên biết là làm thế nào để có được một trạng thái tinh thần tạo ra sự giàu có như thế. Tôi đã dành hai mươi lăm năm để nghiên cứu điều đó vì bản thân tôi cũng muốn biết “những người giàu có đã làm thế nào để đạt được những thành quả như vậy”. Bạn sẽ nhận thấy rằng ngay khi bạn nắm được những triết lí của nguyên tắc thành công này và bắt đầu ứng dụng những nguyên tắc đó, tình hình tài chính của bạn sẽ được cải thiện. Nói một cách hoa mĩ thì mọi thứ bạn chạm tay vào sẽ biến thành vàng. Bạn cho rằng không thể được ư? Thế mà đúng như vậy đấy.

(Nghĩ giàu làm giàu, Napoleon Hill, NXB Thế giới, 2017)

Phương thức biểu đạt chính của đoạn văn trên là gì?

A. Tự sự.

B. Biểu cảm.

C. Miêu tả.

D. Nghị luận.

Xem lời giải

Câu hỏi trong đề: Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 13) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Phương thức biểu đạt chính của đoạn văn là nghị luận. Chọn D.

Câu hỏi cùng đoạn

Câu 2:

Anh/chị hiểu như thế nào về cách diễn đạt: “mọi thứ bạn chạm tay vào sẽ biến thành vàng”?

A. Mục tiêu, nghị lực vượt qua khó khăn.

B. Những việc mà chúng ta làm sẽ đem lại lợi nhuận dễ dàng.

C. Chỉ cần chạm tay, thành công sẽ đến với chúng ta.

D. Kinh nghiệm làm giàu không khó.

Xem lời giải

Lời giải của GV VietJack

“Mọi thứ bạn chạm tay vào sẽ biến thành vàng”: gợi nhớ tích truyện Vua Midas thích vàng, hàm ý chỉ những việc mà chúng ta làm sẽ đem lại lợi nhuận dễ dàng, giống như vua Midas trong câu chuyện, hễ chạm vào đâu là chỗ đó lập tức biến thành vàng. Chọn B.

Câu 3:

Theo anh/chị, trạng thái tinh thần mà tác giả nhắc tới trong đoạn trích là gì?

A. Tình yêu của những người làm giàu và khởi nghiệp.

B. Những gian lao, khó khăn vất vả khi khởi nghiệp và làm giàu.

C. Mục đích rõ ràng khi bắt đầu khởi nghiệp và làm giàu.

D. Những nguy hiểm khi bắt đầu khởi nghiệp và làm giàu.

Xem lời giải

Lời giải của GV VietJack

“Trạng thái tinh thần” mà tác giả nói tới trong đoạn trích có nghĩa là một mục đích rõ ràng khi bắt đầu khởi nghiệp và làm giàu. Trạng thái tinh thần cũng là những yếu tố thuộc về tâm lí của người khởi nghiệp: xác định các phương thức để đạt mục tiêu, nghị lực vượt qua khó khăn, thử thách để đạt được mục tiêu; tâm thế khởi nghiệp... Chọn C.

Câu 4:

Phong cách ngôn ngữ trong đoạn trích trên là gì?

A. Nghệ thuật.

B. Chính luận.

C. Hành chính.

D. Báo chí.

Xem lời giải

Lời giải của GV VietJack

Phong cách ngôn ngữ trong đoạn trích là chính luận. Chọn B.

Câu 5:

Nêu biện pháp tu từ được sử dụng trong câu: Mọi thứ bạn chạm tay vào sẽ biến thành vàng. Bạn cho rằng không thể được ư? Thế mà đúng như vậy đấy.

A. Nói giảm.

B. Nói quá.

C. Nhân hóa.

D. So sánh.

Xem lời giải

Lời giải của GV VietJack

Biện pháp tu từ chính được thể hiện trong câu là nói quá: Mọi thứ bạn chạm tay vào sẽ biến thành vàng. Chọn B.

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{2{\rm{x}} + 2{\rm{ khi x}} \ge 1}\\{3{{\rm{x}}^2} + 1{\rm{ khi }}x < 1}\end{array}} \right..\) Giả sử \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) thoả mãn \(F\left( 0 \right) = 2.\) Giá trị của \(F\left( { - 1} \right) + 2F\left( 2 \right)\) bằng

Xem đáp án

Lời giải

Ta có \(F\left( x \right) = \int f \left( x \right){\rm{d}}x = \left\{ {\begin{array}{*{20}{l}}{{x^2} + 2x + {C_1}}&{{\rm{ khi }}x \ge 1}\\{{x^3} + x + {C_2}}&{{\rm{ khi }}x < 1}\end{array}} \right.\).

Theo bài ra, ta có \(F\left( 0 \right) = 2 \Rightarrow {C_2} = 2\).

Hàm số \(F\left( x \right)\) liên tục nên \(\mathop {\lim }\limits_{x \to {1^ + }} F\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} F\left( x \right)\)

\[ \Leftrightarrow 3 + {C_1} = 4 \Leftrightarrow {C_1} = 1 \Rightarrow F\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{{x^2} + 2x + 1{\rm{ khi }}x \ge 1}\\{{x^3} + x + 2{\rm{ }}\,\,{\rm{khi }}x < 1}\end{array}} \right.\].

Vậy \(F\left( { - 1} \right) + 2F\left( 2 \right) = {\left( { - 1} \right)^3} + \left( { - 1} \right) + 2 + 2 \cdot \left( {{2^2} + 2 \cdot 2 + 1} \right) = 18.\)

Đáp án: 18.

Câu 2

Cho hình lập phương \(ABCD.A'B'C'D'.\) Gọi \(M\) là trung điểm của \(B'C'.\) Góc giữa hai đường thẳng AM và \(BC'\) bằng

A. \(45^\circ .\)

B. \(90^\circ .\)

C. \(30^\circ .\)

D. \(60^\circ .\)

Lời giải

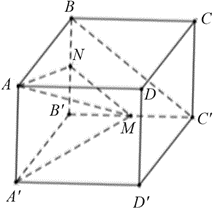
Media VietJack

Giả sử cạnh của hình lập phương là \(a > 0.\)

Gọi \(N\) là trung điểm đoạn thẳng \(BB'.\)

Khi đó, \(MN\,{\rm{//}}\,BC'\) nên \(\left( {\widehat {AM\,;\,\,BC'}} \right) = (\widehat {AM\,;\,MN}).\)

Xét \(\Delta A'B'M\) vuông tại \(B'\), ta có

\(A'M = \sqrt {A'{{B'}^{\prime 2}} + B'{M^2}} = \sqrt {{a^2} + \frac{{{a^2}}}{4}} = \frac{{a\sqrt 5 }}{2}.\)

Xét \(\Delta AA'M\) vuông tại \(A'\), ta có \(AM = \sqrt {A{{A'}^2} + A'{M^2}} = \sqrt {{a^2} + \frac{{5{a^2}}}{4}} = \frac{{3a}}{2}.\)

Có \[AN = A'M = \frac{{a\sqrt 5 }}{2}\,;\,\,MN = \frac{{BC'}}{2} = \frac{{a\sqrt 2 }}{2}.\]

Trong tam giác \[AMN\] ta có

\(\cos \widehat {AMN} = \frac{{M{A^2} + M{N^2} - A{N^2}}}{{2MA \cdot MN}} = \frac{{\frac{{9{a^2}}}{4} + \frac{{2{a^2}}}{4} - \frac{{5{a^2}}}{4}}}{{2 \cdot \frac{{3a}}{2} \cdot \frac{{a\sqrt 2 }}{2}}} = \frac{{6{a^2}}}{4} \cdot \frac{4}{{6{a^2}\sqrt 2 }} = \frac{1}{{\sqrt 2 }}.\)

Suy ra \(\widehat {AMN} = 45^\circ .\) Vậy \[\left( {AM,\,\,BC'} \right) = \left( {AM,\,\,MN} \right) = \widehat {AMN} = 45^\circ .\] Chọn A.

Câu 3