Đọc đoạn trích sau đây và trả lời câu hỏi:

“Lính đảo hát tình ca trên đảo” của Trần Đăng Khoa là một bài thơ hay, để lại ấn tượng sâu sắc từ khi ra đời cho đến nay. Từ cấu tứ, hình ảnh, giọng điệu, tất cả đọc lên cứ vừa tếu táo, bông đùa nhưng lại cảm thương sâu sắc về cuộc đời người lính biển. Họ trở thành tượng đài bất khuất giữa trùng khơi, như một minh chứng cho lòng quả cảm, sự kiên cường của một dân tộc chưa bao giờ khuất phục, sẵn sàng “quyết tử cho Tổ quốc quyết sinh”. Tình ca và hùng ca, hóm hỉnh và lắng đọng, trần trụi và đầy suy tư,... là những trạng thái cảm xúc hài hoà, gắn kết xuyên suốt bài thơ [...] Qua đó, khơi dậy niềm tự hào và tình yêu biển đảo đối với thế hệ trẻ, nhất là ca ngợi vẻ đẹp hào hùng của người lính biển trong vai trò bảo vệ chủ quyền đất nước trong giai đoạn hiện nay.

(Lính đảo hát tình ca trên đảo, Lê Thành Văn)

Đối tượng nào được nhận xét, đánh giá đề cập đến trong đoạn trích trên?

A. Tác giả Trần Đăng Khoa.

B. Bài thơ “Lính đảo hát tình ca trên đảo” của Trần Đăng Khoa.

C. Những người lính đảo.

D. Đảo Trường Sa.

Xem lời giải

Câu hỏi trong đề: Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 13) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đối tượng được nhận xét, đánh giá đề cập đến trong đoạn trích là bài thơ “Lính đảo hát tình ca trên đảo” của Trần Đăng Khoa. Chọn B.

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{2{\rm{x}} + 2{\rm{ khi x}} \ge 1}\\{3{{\rm{x}}^2} + 1{\rm{ khi }}x < 1}\end{array}} \right..\) Giả sử \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) thoả mãn \(F\left( 0 \right) = 2.\) Giá trị của \(F\left( { - 1} \right) + 2F\left( 2 \right)\) bằng

Xem đáp án

Lời giải

Ta có \(F\left( x \right) = \int f \left( x \right){\rm{d}}x = \left\{ {\begin{array}{*{20}{l}}{{x^2} + 2x + {C_1}}&{{\rm{ khi }}x \ge 1}\\{{x^3} + x + {C_2}}&{{\rm{ khi }}x < 1}\end{array}} \right.\).

Theo bài ra, ta có \(F\left( 0 \right) = 2 \Rightarrow {C_2} = 2\).

Hàm số \(F\left( x \right)\) liên tục nên \(\mathop {\lim }\limits_{x \to {1^ + }} F\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} F\left( x \right)\)

\[ \Leftrightarrow 3 + {C_1} = 4 \Leftrightarrow {C_1} = 1 \Rightarrow F\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{{x^2} + 2x + 1{\rm{ khi }}x \ge 1}\\{{x^3} + x + 2{\rm{ }}\,\,{\rm{khi }}x < 1}\end{array}} \right.\].

Vậy \(F\left( { - 1} \right) + 2F\left( 2 \right) = {\left( { - 1} \right)^3} + \left( { - 1} \right) + 2 + 2 \cdot \left( {{2^2} + 2 \cdot 2 + 1} \right) = 18.\)

Đáp án: 18.

Câu 2

Cho hình lập phương \(ABCD.A'B'C'D'.\) Gọi \(M\) là trung điểm của \(B'C'.\) Góc giữa hai đường thẳng AM và \(BC'\) bằng

A. \(45^\circ .\)

B. \(90^\circ .\)

C. \(30^\circ .\)

D. \(60^\circ .\)

Lời giải

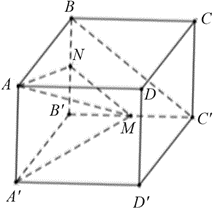
Media VietJack

Giả sử cạnh của hình lập phương là \(a > 0.\)

Gọi \(N\) là trung điểm đoạn thẳng \(BB'.\)

Khi đó, \(MN\,{\rm{//}}\,BC'\) nên \(\left( {\widehat {AM\,;\,\,BC'}} \right) = (\widehat {AM\,;\,MN}).\)

Xét \(\Delta A'B'M\) vuông tại \(B'\), ta có

\(A'M = \sqrt {A'{{B'}^{\prime 2}} + B'{M^2}} = \sqrt {{a^2} + \frac{{{a^2}}}{4}} = \frac{{a\sqrt 5 }}{2}.\)

Xét \(\Delta AA'M\) vuông tại \(A'\), ta có \(AM = \sqrt {A{{A'}^2} + A'{M^2}} = \sqrt {{a^2} + \frac{{5{a^2}}}{4}} = \frac{{3a}}{2}.\)

Có \[AN = A'M = \frac{{a\sqrt 5 }}{2}\,;\,\,MN = \frac{{BC'}}{2} = \frac{{a\sqrt 2 }}{2}.\]

Trong tam giác \[AMN\] ta có

\(\cos \widehat {AMN} = \frac{{M{A^2} + M{N^2} - A{N^2}}}{{2MA \cdot MN}} = \frac{{\frac{{9{a^2}}}{4} + \frac{{2{a^2}}}{4} - \frac{{5{a^2}}}{4}}}{{2 \cdot \frac{{3a}}{2} \cdot \frac{{a\sqrt 2 }}{2}}} = \frac{{6{a^2}}}{4} \cdot \frac{4}{{6{a^2}\sqrt 2 }} = \frac{1}{{\sqrt 2 }}.\)

Suy ra \(\widehat {AMN} = 45^\circ .\) Vậy \[\left( {AM,\,\,BC'} \right) = \left( {AM,\,\,MN} \right) = \widehat {AMN} = 45^\circ .\] Chọn A.

Câu 3