Để tìm hiểu về quá trình hô hấp ở thực vật, một bạn học sinh đã làm thí nghiệm theo đúng quy trình với 50 g hạt đậu đang nảy mầm, nước vôi trong và các dụng cụ thí nghiệm đầy đủ. Nhận định nào sau đây đúng?

A. Thí nghiệm này chỉ thành công khi tiến hành trong điều kiện không có ánh sáng.

B. Nếu thay hạt đang nảy mầm bằng hạt khô thì kết quả thí nghiệm vẫn không thay đổi.

C. Nếu thay nước vôi trong bằng dung dịch xút thì kết quả thí nghiệm cũng giống như sử dụng nước vôi trong.

D. Nước vôi trong bị vẩn đục là do hình thành CaCO3.

Xem lời giải

Câu hỏi trong đề: Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 13) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

A. Sai. Thí nghiệm sử dụng hạt nảy mầm (chưa có khả năng quang hợp) nên vẫn có thể thành công trong điều kiện có ánh sáng.

B. Sai. Cường độ hô hấp ở hạt khô thấp, hạt nảy mầm có cường độ hô hấp cao nên thí nghiệm với hạt khô thì kết quả thí nghiệm sẽ thay đổi.

C. Sai. Dung dịch xút (NaOH) không tạo kết tủa với CO₂.

D. Đúng. Quá trình hô hấp của thực vật thải ra CO₂, CO₂ tạo kết tủa với Ca(OH)₂ làm nước vôi trong bị vẩn đục.

Chọn D.

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{2{\rm{x}} + 2{\rm{ khi x}} \ge 1}\\{3{{\rm{x}}^2} + 1{\rm{ khi }}x < 1}\end{array}} \right..\) Giả sử \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) thoả mãn \(F\left( 0 \right) = 2.\) Giá trị của \(F\left( { - 1} \right) + 2F\left( 2 \right)\) bằng

Xem đáp án

Lời giải

Ta có \(F\left( x \right) = \int f \left( x \right){\rm{d}}x = \left\{ {\begin{array}{*{20}{l}}{{x^2} + 2x + {C_1}}&{{\rm{ khi }}x \ge 1}\\{{x^3} + x + {C_2}}&{{\rm{ khi }}x < 1}\end{array}} \right.\).

Theo bài ra, ta có \(F\left( 0 \right) = 2 \Rightarrow {C_2} = 2\).

Hàm số \(F\left( x \right)\) liên tục nên \(\mathop {\lim }\limits_{x \to {1^ + }} F\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} F\left( x \right)\)

\[ \Leftrightarrow 3 + {C_1} = 4 \Leftrightarrow {C_1} = 1 \Rightarrow F\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{{x^2} + 2x + 1{\rm{ khi }}x \ge 1}\\{{x^3} + x + 2{\rm{ }}\,\,{\rm{khi }}x < 1}\end{array}} \right.\].

Vậy \(F\left( { - 1} \right) + 2F\left( 2 \right) = {\left( { - 1} \right)^3} + \left( { - 1} \right) + 2 + 2 \cdot \left( {{2^2} + 2 \cdot 2 + 1} \right) = 18.\)

Đáp án: 18.

Câu 2

Cho hình lập phương \(ABCD.A'B'C'D'.\) Gọi \(M\) là trung điểm của \(B'C'.\) Góc giữa hai đường thẳng AM và \(BC'\) bằng

A. \(45^\circ .\)

B. \(90^\circ .\)

C. \(30^\circ .\)

D. \(60^\circ .\)

Lời giải

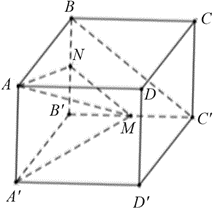
Media VietJack

Giả sử cạnh của hình lập phương là \(a > 0.\)

Gọi \(N\) là trung điểm đoạn thẳng \(BB'.\)

Khi đó, \(MN\,{\rm{//}}\,BC'\) nên \(\left( {\widehat {AM\,;\,\,BC'}} \right) = (\widehat {AM\,;\,MN}).\)

Xét \(\Delta A'B'M\) vuông tại \(B'\), ta có

\(A'M = \sqrt {A'{{B'}^{\prime 2}} + B'{M^2}} = \sqrt {{a^2} + \frac{{{a^2}}}{4}} = \frac{{a\sqrt 5 }}{2}.\)

Xét \(\Delta AA'M\) vuông tại \(A'\), ta có \(AM = \sqrt {A{{A'}^2} + A'{M^2}} = \sqrt {{a^2} + \frac{{5{a^2}}}{4}} = \frac{{3a}}{2}.\)

Có \[AN = A'M = \frac{{a\sqrt 5 }}{2}\,;\,\,MN = \frac{{BC'}}{2} = \frac{{a\sqrt 2 }}{2}.\]

Trong tam giác \[AMN\] ta có

\(\cos \widehat {AMN} = \frac{{M{A^2} + M{N^2} - A{N^2}}}{{2MA \cdot MN}} = \frac{{\frac{{9{a^2}}}{4} + \frac{{2{a^2}}}{4} - \frac{{5{a^2}}}{4}}}{{2 \cdot \frac{{3a}}{2} \cdot \frac{{a\sqrt 2 }}{2}}} = \frac{{6{a^2}}}{4} \cdot \frac{4}{{6{a^2}\sqrt 2 }} = \frac{1}{{\sqrt 2 }}.\)

Suy ra \(\widehat {AMN} = 45^\circ .\) Vậy \[\left( {AM,\,\,BC'} \right) = \left( {AM,\,\,MN} \right) = \widehat {AMN} = 45^\circ .\] Chọn A.

Câu 3