Đọc đoạn trích sau đây và trả lời câu hỏi:
Hồn Trương Ba: (sau một lát) Ông Đế Thích ạ, tôi không thể tiếp tục mang thân anh hàng thịt được nữa, không thể được!
Đế Thích: Sao thế? Có gì không ổn đâu!
Hồn Trương Ba: Không thể bên trong một đằng, bên ngoài một nẻo được. Tôi muốn được là tôi toàn vẹn.
Đế Thích: Thế ông ngỡ tất cả mọi người đều được là mình toàn vẹn ư? Ngay cả tôi đây. Ở bên ngoài, tôi đâu có được sống theo những điều tôi nghĩ bên trong. Mà cả Ngọc Hoàng nữa, chính người lắm khi cũng phải khuôn ép mình cho xứng với danh vị Ngọc Hoàng. Dưới đất, trên trời đều thế cả, nữa là ông. Ông bị gạch tên khỏi sổ Nam Tào. Thân thể thật của ông đã tan rữa trong bùn đất, còn chút hình thù gì của ông đâu!
Hồn Trương Ba: Sống nhờ vào đồ đạc, của cải người khác, đã là chuyện không nên, đằng này đến cái thân tôi cũng phải sống nhờ anh hàng thịt. Ông chỉ nghĩ đơn giản là cho tôi sống, nhưng sống như thế nào thì ông chẳng cần biết!
(Hồn Trương Ba, da hàng thịt – Lưu Quang Vũ)
Câu nói “Không thể bên trong một đằng, bên ngoài một nẻo được. Tôi muốn được là tôi toàn vẹn.” của hồn Trương Ba trong đoạn trích trên có ý nghĩa gì?
Đọc đoạn trích sau đây và trả lời câu hỏi:
Hồn Trương Ba: (sau một lát) Ông Đế Thích ạ, tôi không thể tiếp tục mang thân anh hàng thịt được nữa, không thể được!
Đế Thích: Sao thế? Có gì không ổn đâu!
Hồn Trương Ba: Không thể bên trong một đằng, bên ngoài một nẻo được. Tôi muốn được là tôi toàn vẹn.
Đế Thích: Thế ông ngỡ tất cả mọi người đều được là mình toàn vẹn ư? Ngay cả tôi đây. Ở bên ngoài, tôi đâu có được sống theo những điều tôi nghĩ bên trong. Mà cả Ngọc Hoàng nữa, chính người lắm khi cũng phải khuôn ép mình cho xứng với danh vị Ngọc Hoàng. Dưới đất, trên trời đều thế cả, nữa là ông. Ông bị gạch tên khỏi sổ Nam Tào. Thân thể thật của ông đã tan rữa trong bùn đất, còn chút hình thù gì của ông đâu!
Hồn Trương Ba: Sống nhờ vào đồ đạc, của cải người khác, đã là chuyện không nên, đằng này đến cái thân tôi cũng phải sống nhờ anh hàng thịt. Ông chỉ nghĩ đơn giản là cho tôi sống, nhưng sống như thế nào thì ông chẳng cần biết!
(Hồn Trương Ba, da hàng thịt – Lưu Quang Vũ)
Câu nói “Không thể bên trong một đằng, bên ngoài một nẻo được. Tôi muốn được là tôi toàn vẹn.” của hồn Trương Ba trong đoạn trích trên có ý nghĩa gì?
A. Con người sống phải có khát vọng và lí tưởng.
B. Con người phải có cuộc sống đầy đủ về vật chất và tinh thần.
Quảng cáo
Trả lời:
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x\) (nghìn đồng) là giá phòng khách sạn sau khi tăng giá \((x > 400).\)
Giá chênh lệch sau khi tăng là: \(x - 400\) (nghìn đồng).
Số phòng trống lúc này là: \(2 \cdot \frac{{x - 400}}{{20}} = \frac{{x - 400}}{{10}}\) (phòng).
Số phòng cho thuê lúc này là: \(50 - \frac{{x - 400}}{{10}} = \frac{{900 - x}}{{10}}\) (phòng).
Số tiền phòng thu được là: \(f\left( x \right) = x \cdot \left( {\frac{{900 - x}}{{10}}} \right) = \frac{{ - {x^2} + 900x}}{{10}}\) (nghìn đồng).
Ta cần tìm \(x > 400\) sao cho \(f\left( x \right)\) đạt giá trị lớn nhất.
Dễ thấy \(x = - \frac{{900}}{{2 \cdot ( - 1)}} = 450\) thì lớn nhất. Đáp án: 450.
Câu 2
A. \(T = 6.\)
B. \(T = 0.\)
Lời giải
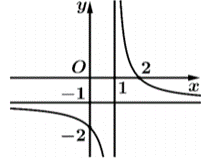
Từ đồ thị ta có:
• TCĐ: \(x = 1 \Rightarrow \frac{{ - d}}{{{c_a}}} = 1 \Rightarrow \frac{d}{c} = - 1 \Rightarrow d = - c\);
• TCN: \(y = - 1 \Rightarrow \frac{a}{c} = - 1 \Rightarrow a = - c\).
Đồ thị cắt trục hoành tại điểm: \(x = 2 \Rightarrow \frac{{ - b}}{a} = 2 \Rightarrow \frac{{ - b}}{{ - c}} = 2 \Rightarrow b = 2c\)
Vậy \(T = \frac{{a - 2b + 3d}}{c} = \frac{{ - c - 4c - 3c}}{c} = - 8\). Chọn C.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(4x - 3y + 18 = 0.\)
B. \(4x - 3y - 18 = 0.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.