Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Thanh Thảo là một gương mặt đầy tâm huyết cho sự đổi mới thơ Việt. Bà đi tìm kiếm những nhân cách tài hoa, những nhân cách bất khuất, những suy nghĩ phóng khoáng, hay ông đến với những người vô danh, lặng thầm mà bất diệt.
Quảng cáo
Trả lời:
Thanh Thảo là tác giả nam. → Thanh Thảo là một gương mặt đầy tâm huyết cho sự đổi mới thơ Việt. Ông đi tìm kiếm những nhân cách tài hoa, những nhân cách bất khuất, những suy nghĩ phóng khoáng, hay ông đến với những người vô danh, lặng thầm mà bất diệt. Chọn A.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
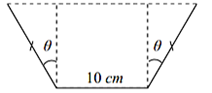
Gọi chiều cao máng nước là: \(h = 10 \cdot \cos \theta \,\,({\rm{cm}})\).
Chiều dài đáy trên máng nước là:
\(10 + 2 \cdot \sqrt {{{10}^2} - {h^2}} = 10 + 2 \cdot \sqrt {{{10}^2} - {{\left( {10 \cdot \cos \theta } \right)}^2}} = 10 + 20 \cdot \sin \theta \,\,({\rm{cm}})\).
Máng nước chứa được nhiều nước nhất khi diện tích hình vẽ lớn nhất
\( \Leftrightarrow S = \frac{{10 + 20 \cdot \sin \theta + 10}}{2} \cdot 10 \cdot \cos \theta = 100 \cdot (1 + \sin \theta ) \cdot \cos \theta = 100 \cdot \left( {\cos \theta + \frac{{\sin 2\theta }}{2}} \right)\).
Ta có \(S' = 100\left( { - \sin \theta + \cos 2\theta } \right) = 100\left( { - \sin \theta + 1 - 2{{\sin }^2}\theta } \right)\)
Khi đó \(S' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\sin \theta = - 1}\\{\sin \theta = \frac{1}{2}}\end{array}} \right.\).
Ta có bảng biến thiên:
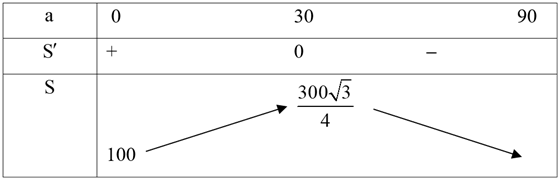
Do đó \({S_{\max }} \Leftrightarrow \sin \theta = \frac{1}{2} \Leftrightarrow \sin \theta = 30^\circ {\rm{.}}\) Đáp án: 30.
Lời giải
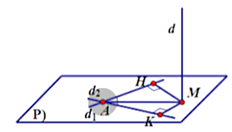
Ta có: \(\overrightarrow {{n_P}} = \left( {1\,;\,\,0\,;\,\, - 1} \right),\,\,\overrightarrow {{u_d}} = \left( { - 1\,;\,\,0\,;\,\,1} \right)\)
\( \Rightarrow d \bot \left( P \right)\) và \(d \cap (P) = M\left( {0\,;\,\,2\,;\,\, - 1} \right)\)
\( \Rightarrow \overrightarrow {MA} = (2; - 1;2) \Rightarrow MA = 3\)
Gọi \[H,\,\,K\] lần lượt là hình chiếu vuông góc của \(M\) lên \({d_1}\) và \({d_2},\) ta có\(d\left( {{d_1}\,;\,\,d} \right) = d\left( {M\,;\,\,{d_1}} \right) = MH,\,\,\,d\left( {{d_2}\,;\,\,d} \right) = d\left( {M\,;\,\,{d_2}} \right) = MK\)
\( \Rightarrow MH = MK = \sqrt 6 \) \( \Rightarrow \sin \widehat {MAK} = \sin \widehat {MAH} = \frac{{HM}}{{AM}} = \frac{{\sqrt 6 }}{3}\)
\( \Rightarrow \cos \left( {{d_1};\,\,{d_2}} \right) = \left| {\cos \left( {2 \cdot \widehat {MAH}} \right)} \right| = \left| {1 - 2{{\sin }^2}\widehat {MAH}} \right| = \left| {1 - \frac{4}{3}} \right| = \frac{1}{3}.\) Đáp án: \(\frac{1}{3}.\)
Câu 3
A. \(S = 4,8.\)
B. \(S = 3,9.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.