Chọn từ/cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Số tranh mang tính chất ________ đơn thuần rất ít, phần lớn là những sáng tác hội họa độc lập dưới âm hưởng của văn học Nam Cao, hoặc là độc lập với cả văn học của Nam Cao, mà những ________ của nhà văn chỉ là cái cớ cho hội họa mà thôi.
Quảng cáo
Trả lời:
Ta nhận thấy chỗ trống thứ nhất có ít sự lựa chọn hơn nên ta tìm từ ngữ thích hợp để điền vào chỗ trống thứ nhất trước.
+ Minh họa: làm rõ thêm, sinh động thêm nội dung muốn trình bày, bằng hình vẽ hoặc những hình thức dễ thấy, dễ hiểu.
+ Khắc họa: miêu tả bằng lời văn một cách đậm nét, rõ ràng, khiến cho nổi bật lên như chạm, vẽ.
Đặt trong nội dung về câu: “Số tranh mang tính chất ______ đơn thuần rất ít”, ta chọn được từ thích hợp để điền vào chỗ trống thứ nhất là “minh họa”.
→ Loại 2 phương án C và D.
Chỗ trống thứ hai với hai từ “quan điểm” và “ý tưởng”:
+ Quan điểm: cách nhìn, cách suy nghĩ.
+ Ý tưởng: những ý nghĩ chưa trọn vẹn, cái bám vào để triển khai một việc gì đó.
Đặt trong nội dung về câu: “những _______ của nhà văn chỉ là cái cớ cho hội họa mà thôi” ta chọn từ thích hợp là “ý tưởng” vì đó chính là cái cớ, cái bám vào để tạo nên những tác phẩm hội họa. Chọn B.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
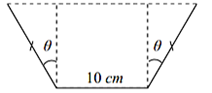
Gọi chiều cao máng nước là: \(h = 10 \cdot \cos \theta \,\,({\rm{cm}})\).
Chiều dài đáy trên máng nước là:
\(10 + 2 \cdot \sqrt {{{10}^2} - {h^2}} = 10 + 2 \cdot \sqrt {{{10}^2} - {{\left( {10 \cdot \cos \theta } \right)}^2}} = 10 + 20 \cdot \sin \theta \,\,({\rm{cm}})\).
Máng nước chứa được nhiều nước nhất khi diện tích hình vẽ lớn nhất
\( \Leftrightarrow S = \frac{{10 + 20 \cdot \sin \theta + 10}}{2} \cdot 10 \cdot \cos \theta = 100 \cdot (1 + \sin \theta ) \cdot \cos \theta = 100 \cdot \left( {\cos \theta + \frac{{\sin 2\theta }}{2}} \right)\).
Ta có \(S' = 100\left( { - \sin \theta + \cos 2\theta } \right) = 100\left( { - \sin \theta + 1 - 2{{\sin }^2}\theta } \right)\)
Khi đó \(S' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\sin \theta = - 1}\\{\sin \theta = \frac{1}{2}}\end{array}} \right.\).
Ta có bảng biến thiên:
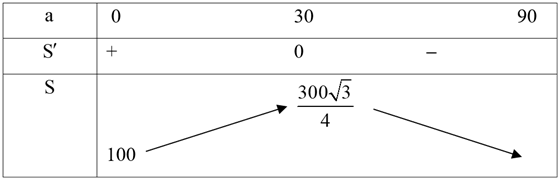
Do đó \({S_{\max }} \Leftrightarrow \sin \theta = \frac{1}{2} \Leftrightarrow \sin \theta = 30^\circ {\rm{.}}\) Đáp án: 30.
Lời giải
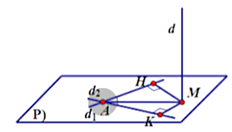
Ta có: \(\overrightarrow {{n_P}} = \left( {1\,;\,\,0\,;\,\, - 1} \right),\,\,\overrightarrow {{u_d}} = \left( { - 1\,;\,\,0\,;\,\,1} \right)\)
\( \Rightarrow d \bot \left( P \right)\) và \(d \cap (P) = M\left( {0\,;\,\,2\,;\,\, - 1} \right)\)
\( \Rightarrow \overrightarrow {MA} = (2; - 1;2) \Rightarrow MA = 3\)
Gọi \[H,\,\,K\] lần lượt là hình chiếu vuông góc của \(M\) lên \({d_1}\) và \({d_2},\) ta có\(d\left( {{d_1}\,;\,\,d} \right) = d\left( {M\,;\,\,{d_1}} \right) = MH,\,\,\,d\left( {{d_2}\,;\,\,d} \right) = d\left( {M\,;\,\,{d_2}} \right) = MK\)
\( \Rightarrow MH = MK = \sqrt 6 \) \( \Rightarrow \sin \widehat {MAK} = \sin \widehat {MAH} = \frac{{HM}}{{AM}} = \frac{{\sqrt 6 }}{3}\)
\( \Rightarrow \cos \left( {{d_1};\,\,{d_2}} \right) = \left| {\cos \left( {2 \cdot \widehat {MAH}} \right)} \right| = \left| {1 - 2{{\sin }^2}\widehat {MAH}} \right| = \left| {1 - \frac{4}{3}} \right| = \frac{1}{3}.\) Đáp án: \(\frac{1}{3}.\)
Câu 3
A. \(S = 4,8.\)
B. \(S = 3,9.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.