Hai bạn Minh và Huy chơi một trò chơi như sau: Minh chọn ngẫu nhiên một số trong tập hợp {5; 6; 7; 8; 9; 10}; Huy chọn ngẫu nhiên một số trong tập hợp {4; 5; 7; 8; 9; 11}. Bạn nào chọn được số lớn hơn sẽ là người thắng cuộc. Nếu hai số chọn được bằng nhau thì kết quả là hoà. Tính xác suất của biến cố sau:
A: “Bạn Minh thắng”;
Hai bạn Minh và Huy chơi một trò chơi như sau: Minh chọn ngẫu nhiên một số trong tập hợp {5; 6; 7; 8; 9; 10}; Huy chọn ngẫu nhiên một số trong tập hợp {4; 5; 7; 8; 9; 11}. Bạn nào chọn được số lớn hơn sẽ là người thắng cuộc. Nếu hai số chọn được bằng nhau thì kết quả là hoà. Tính xác suất của biến cố sau:
A: “Bạn Minh thắng”;
Câu hỏi trong đề: Giải SGK Toán 9 KNTT Bài tập cuối chương 8 có đáp án !!
Quảng cáo
Trả lời:
Phép thử là Minh chọn ngẫu nhiên một số trong tập hợp {5; 6; 7; 8; 9; 10}; Huy chọn ngẫu nhiên một số trong tập hợp {4; 5; 7; 8; 9; 11}.
Kết quả của phép thử là một cặp số (a, b), trong đó a và b tương ứng là số Minh và Huy chọn.
Ta liệt kê được tất cả các kết quả có thể của phép thử bằng cách lập bảng như sau:
|
Huy Minh |
4 |
5 |
7 |
8 |
9 |
11 |
|
5 |
(5, 4) |
(5, 5) |
(5, 7) |
(5, 8) |
(5, 9) |
(5, 11) |
|
6 |
(6, 4) |
(6, 5) |
(6, 7) |
(6, 8) |
(6, 9) |
(6, 11) |
|
7 |
(7, 4) |
(7, 5) |
(7, 7) |
(7, 8) |
(7, 9) |
(7, 11) |
|
8 |
(8, 4) |
(8, 5) |
(8, 7) |
(8, 8) |
(8, 9) |
(8, 11) |
|
9 |
(9, 4) |
(9, 5) |
(9, 7) |
(9, 8) |
(9, 9) |
(9, 11) |
|
10 |
(10, 4) |
(10, 5) |
(10, 7) |
(10, 8) |
(10, 9) |
(10, 11) |
Mỗi ô là một kết quả có thể. Không gian mẫu là tập hợp 36 ô của bảng trên. Do đó, không gian mẫu của phép thử là Ω = {(5, 4); (5, 5); (5, 7); …; (10, 9); (10, 11)}.
Tập Ω có 36 phần tử.
Vì Minh và Huy chọn ngẫu nhiên một số nên các kết quả có thể xảy ra ở trên là đồng khả năng.
Có 17 kết quả thuận lợi của biến cố A là: (5, 4); (6, 4); (6, 5); (7, 4); (7, 5); (8, 4); (8, 5); (8, 7); (9, 4); (9, 5); (9, 7); (9, 8); (10, 4); (10, 5); (10, 7); (10, 8); (10, 9). Do đó, 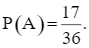
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: B
Phép thử là lấy ngẫu nhiên hai viên bi từ trong túi.
Kết quả của phép thử là (a, b), trong đó a và b tương ứng là các số trên hai viên bi trong túi. Vì lấy đồng thời 2 viên bi nên a ≠ b.
Do đó, không gian mẫu là: Ω = {(1, 2); (1, 3); (1, 4); (2, 3); (2, 4); (3, 4)}.
Không gian mẫu Ω có 6 phần tử.
Vì lấy ngẫu nhiên hai viên bi từ trong túi nên các kết quả có thể xảy ra ở trên là đồng khả năng.
Có 4 kết quả thuận lợi của biến cố A: “Tích hai số ghi trên hai viên bi lớn hơn 3” là: (1, 4); (2, 3); (2, 4); (3, 4). Do đó, 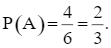
Lời giải
Phép thử là rút ngẫu nhiên một thẻ từ mỗi túi I và II.
Kết quả của phép thử là một cặp số (a, b), trong đó a và b tương ứng là số ghi trên tấm thẻ được lấy từ túi I và túi II.
Ta liệt kê được tất cả các kết quả có thể của phép thử bằng cách lập bảng như sau:
|
Túi II Túi I |
5 |
6 |
|
2 |
(2, 5) |
(2, 6) |
|
3 |
(3, 5) |
(3, 6) |
|
4 |
(4, 5) |
(4, 6) |
Mỗi ô là một kết quả có thể. Không gian mẫu là tập hợp 6 ô của bảng trên. Do đó, không gian mẫu của phép thử là Ω = {(2, 5); (2, 6); (3, 5); (3, 6); (4, 5); (4, 6)}.
Tập Ω có 6 phần tử.
Vì rút ngẫu nhiên một tấm thẻ từ mỗi túi I và II nên các kết quả có thể xảy ra ở trên là đồng khả năng.
⦁ Có 2 kết quả thuận lợi của biến cố A là: (3, 5); (4, 6). Do đó, 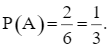
⦁ Có 3 kết quả thuận lợi của biến cố B là: (2, 5); (2, 6); (3, 6). Do đó, 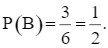
⦁ Có 5 kết quả thuận lợi của biến cố C là: (2, 5); (2, 6); (3, 6); (4, 5); (4, 6). Do đó, 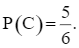
⦁ Có 1 kết quả thuận lợi của biến cố D là: (2, 5). Do đó, 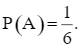
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.