Giải SGK Toán 9 KNTT Bài tập cuối chương 8 có đáp án
28 người thi tuần này 4.6 460 lượt thi 7 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án
Danh sách câu hỏi:
Lời giải
Đáp án đúng là: C
Phép thử là gieo đồng thời hai con xúc xắc cân đối và đồng chất.
Kết quả của phép thử là (a, b), trong đó a và b tương ứng là số chấm xuất hiện trên con xúc xắc thứ nhất và thứ hai.
Ta liệt kê được tất cả các kết quả có thể của phép thử bằng cách lập bảng như sau:
|
Xúc xắc thứ hai Xúc xắc thứ nhất |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
(1, 1) |
(1, 2) |
(1, 3) |
(1, 4) |
(1, 5) |
(1, 6) |
|
2 |
(2, 1) |
(2, 2) |
(2, 3) |
(2, 4) |
(2, 5) |
(2, 6) |
|
3 |
(3, 1) |
(3, 2) |
(3, 3) |
(3, 4) |
(3, 5) |
(3, 6) |
|
4 |
(4, 1) |
(4, 2) |
(4, 3) |
(4, 4) |
(4, 5) |
(4, 6) |
|
5 |
(5, 1) |
(5, 2) |
(5, 3) |
(5, 4) |
(5, 5) |
(5, 6) |
|
6 |
(6, 1) |
(6, 2) |
(6, 3) |
(6, 4) |
(6, 5) |
(6, 6) |
Mỗi ô là một kết quả có thể. Không gian mẫu là tập hợp 36 ô của bảng trên. Do đó, không gian mẫu của phép thử là Ω = {(1, 1); (1, 2); (1, 3); …; (5, 6); (6, 6)}.
Tập Ω có 36 phần tử.
Vì gieo đồng thời hai con xúc xắc cân đối, đồng chất nên các kết quả có thể xảy ra là đồng khả năng.
Có 6 kết quả thuận lợi của biến cố A: “Tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn hoặc bằng 10” là: (4, 6); (5, 5); (5, 6); (6, 4); (6, 5); (6, 6).
Do đó, 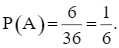
Lời giải
Đáp án đúng là: A
Phép thử là rút ngẫu nhiên một tấm thẻ từ mỗi túi I và II.
Kết quả của phép thử là (a, b), trong đó a và b tương ứng là số ghi trên tấm thẻ rút từ túi I và túi II.
Ta liệt kê được tất cả các kết quả có thể của phép thử bằng cách lập bảng như sau:
|
Túi II Túi I |
1 |
2 |
3 |
4 |
5 |
|
1 |
(1, 1) |
(1, 2) |
(1, 3) |
(1, 4) |
(1, 5) |
|
2 |
(2, 1) |
(2, 2) |
(2, 3) |
(2, 4) |
(2, 5) |
|
3 |
(3, 1) |
(3, 2) |
(3, 3) |
(3, 4) |
(3, 5) |
|
4 |
(4, 1) |
(4, 2) |
(4, 3) |
(4, 4) |
(4, 5) |
Mỗi ô là một kết quả có thể. Không gian mẫu là tập hợp 20 ô của bảng trên. Do đó, không gian mẫu của phép thử là Ω = {(1, 1); (1, 2); (1, 3); …; (4, 4); (4, 5)}.
Tập Ω có 20 phần tử.
Vì rút ngẫu nhiên một tấm thẻ từ mỗi túi I và II nên các kết quả có thể xảy ra ở trên là đồng khả năng.
Có 4 kết quả thuận lợi của biến cố A: “Cả hai tấm thẻ rút ra đều ghi số chẵn” là: (2, 2); (2, 4); (4, 2); (4, 4). Do đó, 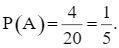
Lời giải
Đáp án đúng là: B
Phép thử là lấy ngẫu nhiên hai viên bi từ trong túi.
Kết quả của phép thử là (a, b), trong đó a và b tương ứng là các số trên hai viên bi trong túi. Vì lấy đồng thời 2 viên bi nên a ≠ b.
Do đó, không gian mẫu là: Ω = {(1, 2); (1, 3); (1, 4); (2, 3); (2, 4); (3, 4)}.
Không gian mẫu Ω có 6 phần tử.
Vì lấy ngẫu nhiên hai viên bi từ trong túi nên các kết quả có thể xảy ra ở trên là đồng khả năng.
Có 4 kết quả thuận lợi của biến cố A: “Tích hai số ghi trên hai viên bi lớn hơn 3” là: (1, 4); (2, 3); (2, 4); (3, 4). Do đó, 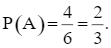
Lời giải
Phép thử là rút ngẫu nhiên một thẻ từ mỗi túi I và II.
Kết quả của phép thử là một cặp số (a, b), trong đó a và b tương ứng là số ghi trên tấm thẻ được lấy từ túi I và túi II.
Ta liệt kê được tất cả các kết quả có thể của phép thử bằng cách lập bảng như sau:
|
Túi II Túi I |
5 |
6 |
|
2 |
(2, 5) |
(2, 6) |
|
3 |
(3, 5) |
(3, 6) |
|
4 |
(4, 5) |
(4, 6) |
Mỗi ô là một kết quả có thể. Không gian mẫu là tập hợp 6 ô của bảng trên. Do đó, không gian mẫu của phép thử là Ω = {(2, 5); (2, 6); (3, 5); (3, 6); (4, 5); (4, 6)}.
Tập Ω có 6 phần tử.
Vì rút ngẫu nhiên một tấm thẻ từ mỗi túi I và II nên các kết quả có thể xảy ra ở trên là đồng khả năng.
⦁ Có 2 kết quả thuận lợi của biến cố A là: (3, 5); (4, 6). Do đó, 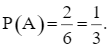
⦁ Có 3 kết quả thuận lợi của biến cố B là: (2, 5); (2, 6); (3, 6). Do đó, 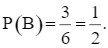
⦁ Có 5 kết quả thuận lợi của biến cố C là: (2, 5); (2, 6); (3, 6); (4, 5); (4, 6). Do đó, 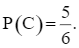
⦁ Có 1 kết quả thuận lợi của biến cố D là: (2, 5). Do đó, 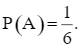
Lời giải
Phép thử là gieo đồng thời hai con xúc xắc cân đối, đồng chất I và II.
Kết quả của phép thử là (a, b), trong đó a và b tương ứng là số chấm xuất hiện trên con xúc xắc I và con xúc xắc II.
Ta liệt kê được tất cả các kết quả có thể của phép thử bằng cách lập bảng như sau:
|
Xúc xắc II Xúc xắc I |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
(1, 1) |
(1, 2) |
(1, 3) |
(1, 4) |
(1, 5) |
(1, 6) |
|
2 |
(2, 1) |
(2, 2) |
(2, 3) |
(2, 4) |
(2, 5) |
(2, 6) |
|
3 |
(3, 1) |
(3, 2) |
(3, 3) |
(3, 4) |
(3, 5) |
(3, 6) |
|
4 |
(4, 1) |
(4, 2) |
(4, 3) |
(4, 4) |
(4, 5) |
(4, 6) |
|
5 |
(5, 1) |
(5, 2) |
(5, 3) |
(5, 4) |
(5, 5) |
(5, 6) |
|
6 |
(6, 1) |
(6, 2) |
(6, 3) |
(6, 4) |
(6, 5) |
(6, 6) |
Mỗi ô là một kết quả có thể. Không gian mẫu là tập hợp 36 ô của bảng trên. Do đó, không gian mẫu của phép thử là Ω = {(1, 1); (1, 2); (1, 3); …; (6, 5); (6, 6)}.
Tập Ω có 36 phần tử.
Vì gieo đồng thời hai con xúc xắc cân đối, đồng chất nên các kết quả có thể xảy ra là đồng khả năng.
⦁ Có 2 kết quả thuận lợi của biến cố E là: (5, 6); (6, 5). Do đó, 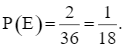
⦁ Có 9 kết quả thuận lợi của biến cố F là: (2, 6); (3, 5); (3, 6); (4, 4); (4, 5); (5, 3); (5, 4); (6, 2); (6, 3). Do đó, 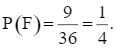
⦁ Có 10 kết quả thuận lợi của biến cố G là: (1, 1); (1, 2); (1, 3); (1, 4); (2, 1); (2, 2); (2, 3); (3, 1); (3, 2); (4, 1). Do đó, 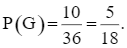
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.