Năm 1736, nhà bác học Euler đưa ra bài toán, được gọi là bài toán 7 cây cầu ở Königsberg. Tại thành phố cổ Königsberg của nước Phổ cũ (nay thuộc nước Nga) có dòng sông Pregel vắt ngang qua, chia thành phố thành các vùng riêng biệt. Bài toán Euler đặt ra là làm sao đi qua tất cả 7 cây cầu này, mỗi cầu chỉ được phép đi qua đúng một lần.
Em hãy giải bài toán trên.
Có thể dùng mô hình dữ liệu nào để mô phỏng bài toán này?
Năm 1736, nhà bác học Euler đưa ra bài toán, được gọi là bài toán 7 cây cầu ở Königsberg. Tại thành phố cổ Königsberg của nước Phổ cũ (nay thuộc nước Nga) có dòng sông Pregel vắt ngang qua, chia thành phố thành các vùng riêng biệt. Bài toán Euler đặt ra là làm sao đi qua tất cả 7 cây cầu này, mỗi cầu chỉ được phép đi qua đúng một lần.
Em hãy giải bài toán trên.
Có thể dùng mô hình dữ liệu nào để mô phỏng bài toán này?
Quảng cáo
Trả lời:
Bài toán 7 cây cầu ở Königsberg có thể được giải bằng một số phương pháp, trong đó một phương pháp hiệu quả là sử dụng đồ thị. Mô hình đồ thị có thể được sử dụng để mô phỏng bài toán này.
Một cách tiếp cận đơn giản là sử dụng đồ thị vô hướng, trong đó mỗi cầu được biểu diễn bởi một cạnh của đồ thị, và mỗi khu vực của thành phố được biểu diễn bởi một đỉnh. Bài toán trở thành việc tìm một đường đi qua tất cả các cầu (cạnh) một lần và quay lại nút xuất phát (đỉnh xuất phát).
Một cách khác để mô hình hóa bài toán này là sử dụng cây tìm kiếm nhị phân. Mỗi nút trong cây có thể biểu diễn một câu chuyện từ điểm xuất phát đến các cây cầu, trong đó mỗi cầu được đi qua một lần. Bằng cách này, ta có thể tìm kiếm một đường đi hợp lệ (nếu tồn tại) từ điểm xuất phát đến các cây cầu và quay lại điểm xuất phát.
Tùy thuộc vào cách tiếp cận, mô hình dữ liệu sẽ thay đổi. Đối với mô hình đồ thị, ta có thể sử dụng ma trận kề hoặc danh sách kề để biểu diễn đồ thị. Đối với mô hình cây tìm kiếm nhị phân, mỗi nút có thể lưu trữ thông tin về cầu đã đi qua và các khu vực đã được ghé thăm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sổ tay Giáo dục Kinh tế & Pháp luật 12 (chương trình mới) ( 18.000₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
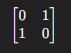
Để vẽ và thiết lập ma trận kề của đồ thị đầy đủ với số đỉnh n=2,3,4 ta sẽ xác định tất cả các cạnh có thể nối giữa các đỉnh.
1. Khi n=2:
- Đồ thị chỉ có hai đỉnh V={0,1}
- Vì đồ thị đầy đủ, nên có một cạnh nối giữa mọi cặp đỉnh.
- Ma trận kề sẽ có dạng:
2. Khi n=3:
- Đồ thị có ba đỉnh V={0,1,2}.
- Tương tự như trường hợp trên, có một cạnh nối giữa mọi cặp đỉnh.
- Ma trận kề:

3. Khi n=4:
- Đồ thị có bốn đỉnh V={0,1,2,3}.
- Đồ thị đầy đủ có một cạnh nối giữa mọi cặp đỉnh.
- Ma trận kề:

Trong ma trận kề, giá trị 1 ở hàng i và cột j thể hiện rằng có một cạnh nối giữa đỉnh i và đỉnh j.
Lời giải
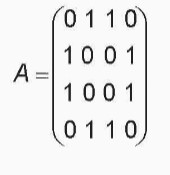
Xét từng hàng của ma trận kề:
- Hàng 1: Đỉnh 0 kề với đỉnh 1 và 2.
- Hàng 2: Đỉnh 1 kề với đỉnh 0 và 3.
- Hàng 3: Đỉnh 2 kề với đỉnh 0 và 3.
- Hàng 4: Đỉnh 3 kề với đỉnh 1 và 2.
Dựa trên thông tin này, ta có thể vẽ đồ thị như sau:
Xét từng hàng của ma trận kề:
- Hàng 1: Đỉnh 0 kề với đỉnh 1 và 2.
- Hàng 2: Đỉnh 1 kề với đỉnh 0 và 3.
- Hàng 3: Đỉnh 2 kề với đỉnh 0 và 3.
- Hàng 4: Đỉnh 3 kề với đỉnh 1 và 2.
Dựa trên thông tin này, ta có thể vẽ đồ thị như sau:

Trong đồ thị này, mỗi đỉnh được biểu diễn bởi một số, và mỗi cạnh giữa các đỉnh được biểu diễn bằng các đoạn thẳng nối hai đỉnh tương ứng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.