Giải chuyên đề Tin 12 KNTT Bài 11: Khái niệm đồ thị có đáp án

Bài toán 7 cây cầu ở Königsberg có thể được giải bằng một số phương pháp, trong đó một phương pháp hiệu quả là sử dụng đồ thị. Mô hình đồ thị có thể được sử dụng để mô phỏng bài toán này.

Một cách tiếp cận đơn giản là sử dụng đồ thị vô hướng, trong đó mỗi cầu được biểu diễn bởi một cạnh của đồ thị, và mỗi khu vực của thành phố được biểu diễn bởi một đỉnh. Bài toán trở thành việc tìm một đường đi qua tất cả các cầu (cạnh) một lần và quay lại nút xuất phát (đỉnh xuất phát).

Một cách khác để mô hình hóa bài toán này là sử dụng cây tìm kiếm nhị phân. Mỗi nút trong cây có thể biểu diễn một câu chuyện từ điểm xuất phát đến các cây cầu, trong đó mỗi cầu được đi qua một lần. Bằng cách này, ta có thể tìm kiếm một đường đi hợp lệ (nếu tồn tại) từ điểm xuất phát đến các cây cầu và quay lại điểm xuất phát.

Tùy thuộc vào cách tiếp cận, mô hình dữ liệu sẽ thay đổi. Đối với mô hình đồ thị, ta có thể sử dụng ma trận kề hoặc danh sách kề để biểu diễn đồ thị. Đối với mô hình cây tìm kiếm nhị phân, mỗi nút có thể lưu trữ thông tin về cầu đã đi qua và các khu vực đã được ghé thăm.

1. Mô hình đồ thị là một cách mạnh mẽ để mô tả một tập hợp các đối tượng (đỉnh) và các mối quan hệ giữa chúng (cạnh). Đồ thị có thể có các biến thể khác nhau như đồ thị vô hướng, đồ thị có hướng, đồ thị có trọng số, và đồ thị có hướng và trọng số.
Bài toán trong phần khởi động, cụ thể là bài toán 7 cây cầu ở Königsberg, có thể biểu diễn được bằng mô hình đồ thị. Trong mô hình này, mỗi khu vực của thành phố sẽ được biểu diễn bởi một đỉnh, và mỗi cây cầu sẽ được biểu diễn bởi một cạnh. Với mỗi cầu, ta có thể có một cạnh vô hướng nối hai đỉnh biểu diễn hai khu vực mà cầu đó nối.
Bằng cách này, ta có thể sử dụng các thuật toán trên đồ thị để giải quyết bài toán, chẳng hạn như thuật toán DFS (Depth-First Search) hoặc BFS (Breadth-First Search) để kiểm tra xem có đường đi qua tất cả các cầu một lần hay không.

2. Có nhiều bài toán thực tế khác mà có thể biểu diễn bằng mô hình đồ thị. Dưới đây là một số ví dụ:

- Mạng lưới điện: Trong một mạng lưới điện, các trạm biến áp và đường dây truyền điện có thể được biểu diễn bằng các đỉnh và cạnh trong đồ thị. Việc phân tích mạng lưới điện có thể giúp tối ưu hóa việc phân phối điện năng.

- Mạng xã hội: Trong mạng xã hội, mỗi cá nhân có thể được biểu diễn bằng một đỉnh và mối quan hệ giữa các cá nhân có thể được biểu diễn bằng các cạnh. Đồ thị của mạng xã hội có thể được sử dụng để phân tích mối quan hệ, tìm kiếm những cá nhân quan trọng, hoặc dự đoán sự lan truyền của thông tin.

- Mạng giao thông: Trong mạng giao thông, các nút giao thông và các tuyến đường có thể được biểu diễn bằng các đỉnh và cạnh trong đồ thị. Việc phân tích mạng giao thông có thể giúp tối ưu hóa lộ trình đi lại, dự đoán tình trạng giao thông, hoặc thiết kế hệ thống giao thông hiệu quả hơn.

Cây, cây nhị phân và cây tìm kiếm nhị phân không phải là mô hình đồ thị trong định nghĩa cơ bản của đồ thị. Tuy nhiên, chúng có mối liên quan với đồ thị thông qua một số khái niệm và biến thể.

1. Cây: Trong lý thuyết đồ thị, một cây là một loại đồ thị vô hướng không chứa chu trình. Cây có thể được biểu diễn dưới dạng một đồ thị đặc biệt, trong đó mỗi nút có đúng một nút cha trừ nút gốc, và không có chu trình.

2. Cây nhị phân: Cây nhị phân là một loại cây trong đó mỗi nút có tối đa hai con, được gọi là con trái và con phải. Mỗi nút trong cây nhị phân đều có mối quan hệ với nút cha của nó, tạo thành một cấu trúc phân cấp. Mặc dù cây nhị phân không phải là đồ thị theo định nghĩa chính thức, nhưng nó có thể được biểu diễn bằng đồ thị với một số ràng buộc, chẳng hạn như mỗi nút chỉ có thể có tối đa hai con.

3. Cây tìm kiếm nhị phân: Cây tìm kiếm nhị phân là một loại cây nhị phân đặc biệt, trong đó mỗi nút chứa một giá trị (phần tử) và được sắp xếp theo thứ tự sao cho mọi giá trị ở cây con trái nhỏ hơn giá trị của nút cha và mọi giá trị ở cây con phải lớn hơn giá trị của nút cha. Cây tìm kiếm nhị phân cũng có thể được coi là một biến thể của đồ thị, với mỗi nút là một đỉnh và mối quan hệ giữa các nút được xác định bởi thứ tự giá trị của chúng.

Như vậy, mặc dù cây, cây nhị phân và cây tìm kiếm nhị phân không phải là đồ thị trong định nghĩa chính thức, nhưng chúng có mối quan hệ mật thiết với đồ thị thông qua một số khái niệm và biến thể, và có thể được mô phỏng hoặc biểu diễn dưới dạng đồ thị.

Để vẽ đồ thị vô hướng G = (V, E) có các đỉnh V = [0, 1, 2, 3, 4] và các cạnh E = [{0,1}, {0,4}, {1,2}, {1,3}, {2,4}], chúng ta sẽ vẽ các đỉnh và các cạnh tương ứng. 

Đầu tiên, vẽ các đỉnh:

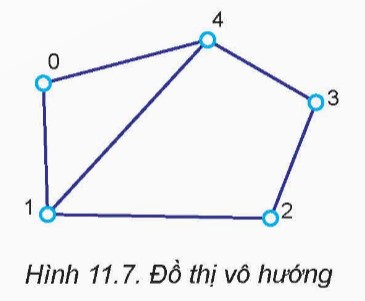
Dựa trên hình ảnh bạn đã cung cấp, đây là mô tả của tập hợp đỉnh ( V ) và tập hợp cạnh ( E ) cho đồ thị vô hướng trong Hình 11.7:

Tập hợp đỉnh ( V ): ( V = {0, 1, 2, 3, 4} )

Tập hợp cạnh ( E ): ( E = {(0,1), (1,2), (2,3), (3,4), (4,0), (0,2)} )

Mỗi cạnh được biểu diễn bằng một cặp đỉnh mà nó kết nối, và vì đồ thị là vô hướng, không có mũi tên chỉ hướng trên các cạnh.