Câu hỏi trong đề: Giải SGK Chuyên đề Tin học 12 Bài 11. Khái niệm đồ thị !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Cây, cây nhị phân và cây tìm kiếm nhị phân không phải là mô hình đồ thị trong định nghĩa cơ bản của đồ thị. Tuy nhiên, chúng có mối liên quan với đồ thị thông qua một số khái niệm và biến thể.
1. Cây: Trong lý thuyết đồ thị, một cây là một loại đồ thị vô hướng không chứa chu trình. Cây có thể được biểu diễn dưới dạng một đồ thị đặc biệt, trong đó mỗi nút có đúng một nút cha trừ nút gốc, và không có chu trình.
2. Cây nhị phân: Cây nhị phân là một loại cây trong đó mỗi nút có tối đa hai con, được gọi là con trái và con phải. Mỗi nút trong cây nhị phân đều có mối quan hệ với nút cha của nó, tạo thành một cấu trúc phân cấp. Mặc dù cây nhị phân không phải là đồ thị theo định nghĩa chính thức, nhưng nó có thể được biểu diễn bằng đồ thị với một số ràng buộc, chẳng hạn như mỗi nút chỉ có thể có tối đa hai con.
3. Cây tìm kiếm nhị phân: Cây tìm kiếm nhị phân là một loại cây nhị phân đặc biệt, trong đó mỗi nút chứa một giá trị (phần tử) và được sắp xếp theo thứ tự sao cho mọi giá trị ở cây con trái nhỏ hơn giá trị của nút cha và mọi giá trị ở cây con phải lớn hơn giá trị của nút cha. Cây tìm kiếm nhị phân cũng có thể được coi là một biến thể của đồ thị, với mỗi nút là một đỉnh và mối quan hệ giữa các nút được xác định bởi thứ tự giá trị của chúng.
Như vậy, mặc dù cây, cây nhị phân và cây tìm kiếm nhị phân không phải là đồ thị trong định nghĩa chính thức, nhưng chúng có mối quan hệ mật thiết với đồ thị thông qua một số khái niệm và biến thể, và có thể được mô phỏng hoặc biểu diễn dưới dạng đồ thị.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Để vẽ và thiết lập ma trận kề của đồ thị đầy đủ với số đỉnh n=2,3,4 ta sẽ xác định tất cả các cạnh có thể nối giữa các đỉnh.
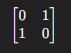
1. Khi n=2:
- Đồ thị chỉ có hai đỉnh V={0,1}
- Vì đồ thị đầy đủ, nên có một cạnh nối giữa mọi cặp đỉnh.
- Ma trận kề sẽ có dạng:
2. Khi n=3:
- Đồ thị có ba đỉnh V={0,1,2}.
- Tương tự như trường hợp trên, có một cạnh nối giữa mọi cặp đỉnh.
- Ma trận kề:
3. Khi n=4:
- Đồ thị có bốn đỉnh V={0,1,2,3}.
- Đồ thị đầy đủ có một cạnh nối giữa mọi cặp đỉnh.
- Ma trận kề:
Trong ma trận kề, giá trị 1 ở hàng i và cột j thể hiện rằng có một cạnh nối giữa đỉnh i và đỉnh j.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
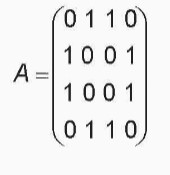
Xét từng hàng của ma trận kề:
- Hàng 1: Đỉnh 0 kề với đỉnh 1 và 2.
- Hàng 2: Đỉnh 1 kề với đỉnh 0 và 3.
- Hàng 3: Đỉnh 2 kề với đỉnh 0 và 3.
- Hàng 4: Đỉnh 3 kề với đỉnh 1 và 2.
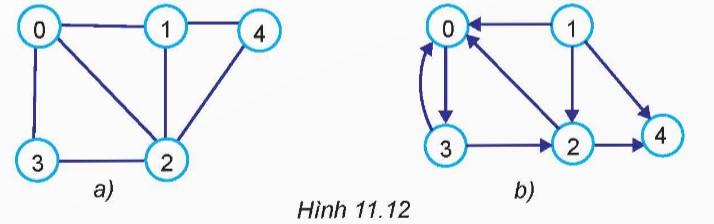
Dựa trên thông tin này, ta có thể vẽ đồ thị như sau:
Xét từng hàng của ma trận kề:
- Hàng 1: Đỉnh 0 kề với đỉnh 1 và 2.
- Hàng 2: Đỉnh 1 kề với đỉnh 0 và 3.
- Hàng 3: Đỉnh 2 kề với đỉnh 0 và 3.
- Hàng 4: Đỉnh 3 kề với đỉnh 1 và 2.
Dựa trên thông tin này, ta có thể vẽ đồ thị như sau:
Trong đồ thị này, mỗi đỉnh được biểu diễn bởi một số, và mỗi cạnh giữa các đỉnh được biểu diễn bằng các đoạn thẳng nối hai đỉnh tương ứng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập