1. Trao đổi, thảo luận về mô hình đồ thị, các khái niệm cơ bản của đồ thị và trả lời câu hỏi: Bài toán trong phần khởi động có thể biểu diễn được bằng mô hình đồ thị không?
2. Em hãy tìm một số bài toán thực tế khác có thể biểu diễn được bằng đồ thị.
1. Trao đổi, thảo luận về mô hình đồ thị, các khái niệm cơ bản của đồ thị và trả lời câu hỏi: Bài toán trong phần khởi động có thể biểu diễn được bằng mô hình đồ thị không?
2. Em hãy tìm một số bài toán thực tế khác có thể biểu diễn được bằng đồ thị.
Quảng cáo
Trả lời:
1. Mô hình đồ thị là một cách mạnh mẽ để mô tả một tập hợp các đối tượng (đỉnh) và các mối quan hệ giữa chúng (cạnh). Đồ thị có thể có các biến thể khác nhau như đồ thị vô hướng, đồ thị có hướng, đồ thị có trọng số, và đồ thị có hướng và trọng số.
Bài toán trong phần khởi động, cụ thể là bài toán 7 cây cầu ở Königsberg, có thể biểu diễn được bằng mô hình đồ thị. Trong mô hình này, mỗi khu vực của thành phố sẽ được biểu diễn bởi một đỉnh, và mỗi cây cầu sẽ được biểu diễn bởi một cạnh. Với mỗi cầu, ta có thể có một cạnh vô hướng nối hai đỉnh biểu diễn hai khu vực mà cầu đó nối.
Bằng cách này, ta có thể sử dụng các thuật toán trên đồ thị để giải quyết bài toán, chẳng hạn như thuật toán DFS (Depth-First Search) hoặc BFS (Breadth-First Search) để kiểm tra xem có đường đi qua tất cả các cầu một lần hay không.
2. Có nhiều bài toán thực tế khác mà có thể biểu diễn bằng mô hình đồ thị. Dưới đây là một số ví dụ:
- Mạng lưới điện: Trong một mạng lưới điện, các trạm biến áp và đường dây truyền điện có thể được biểu diễn bằng các đỉnh và cạnh trong đồ thị. Việc phân tích mạng lưới điện có thể giúp tối ưu hóa việc phân phối điện năng.
- Mạng xã hội: Trong mạng xã hội, mỗi cá nhân có thể được biểu diễn bằng một đỉnh và mối quan hệ giữa các cá nhân có thể được biểu diễn bằng các cạnh. Đồ thị của mạng xã hội có thể được sử dụng để phân tích mối quan hệ, tìm kiếm những cá nhân quan trọng, hoặc dự đoán sự lan truyền của thông tin.
- Mạng giao thông: Trong mạng giao thông, các nút giao thông và các tuyến đường có thể được biểu diễn bằng các đỉnh và cạnh trong đồ thị. Việc phân tích mạng giao thông có thể giúp tối ưu hóa lộ trình đi lại, dự đoán tình trạng giao thông, hoặc thiết kế hệ thống giao thông hiệu quả hơn.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sổ tay Giáo dục Kinh tế & Pháp luật 12 (chương trình mới) ( 18.000₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Để vẽ và thiết lập ma trận kề của đồ thị đầy đủ với số đỉnh n=2,3,4 ta sẽ xác định tất cả các cạnh có thể nối giữa các đỉnh.
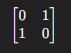
1. Khi n=2:
- Đồ thị chỉ có hai đỉnh V={0,1}
- Vì đồ thị đầy đủ, nên có một cạnh nối giữa mọi cặp đỉnh.
- Ma trận kề sẽ có dạng:
2. Khi n=3:
- Đồ thị có ba đỉnh V={0,1,2}.
- Tương tự như trường hợp trên, có một cạnh nối giữa mọi cặp đỉnh.
- Ma trận kề:

3. Khi n=4:
- Đồ thị có bốn đỉnh V={0,1,2,3}.
- Đồ thị đầy đủ có một cạnh nối giữa mọi cặp đỉnh.
- Ma trận kề:

Trong ma trận kề, giá trị 1 ở hàng i và cột j thể hiện rằng có một cạnh nối giữa đỉnh i và đỉnh j.
Lời giải
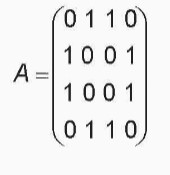
Xét từng hàng của ma trận kề:
- Hàng 1: Đỉnh 0 kề với đỉnh 1 và 2.
- Hàng 2: Đỉnh 1 kề với đỉnh 0 và 3.
- Hàng 3: Đỉnh 2 kề với đỉnh 0 và 3.
- Hàng 4: Đỉnh 3 kề với đỉnh 1 và 2.
Dựa trên thông tin này, ta có thể vẽ đồ thị như sau:
Xét từng hàng của ma trận kề:
- Hàng 1: Đỉnh 0 kề với đỉnh 1 và 2.
- Hàng 2: Đỉnh 1 kề với đỉnh 0 và 3.
- Hàng 3: Đỉnh 2 kề với đỉnh 0 và 3.
- Hàng 4: Đỉnh 3 kề với đỉnh 1 và 2.
Dựa trên thông tin này, ta có thể vẽ đồ thị như sau:

Trong đồ thị này, mỗi đỉnh được biểu diễn bởi một số, và mỗi cạnh giữa các đỉnh được biểu diễn bằng các đoạn thẳng nối hai đỉnh tương ứng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.