Câu hỏi:
11/07/2024 156
Đọc, trao đổi và thảo luận các khái niệm, định nghĩa liên quan đến đồ thị. Quan sát đồ thị ở Hình 11.8 và thực hiện các yêu cầu sau:
1. Kể tên các đỉnh kề với D.
2. Hãy cho biết bậc của đỉnh A.
3. Liệt kê một vài đường đi từ đỉnh A đến đỉnh E.
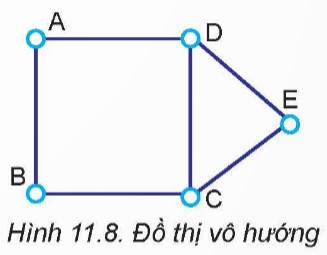
Đọc, trao đổi và thảo luận các khái niệm, định nghĩa liên quan đến đồ thị. Quan sát đồ thị ở Hình 11.8 và thực hiện các yêu cầu sau:
1. Kể tên các đỉnh kề với D.
2. Hãy cho biết bậc của đỉnh A.
3. Liệt kê một vài đường đi từ đỉnh A đến đỉnh E.
Quảng cáo
Trả lời:
Giải bởi Vietjack
1. Các đỉnh kề với D: Đỉnh D kề với các đỉnh A, C và E.
2. Bậc của đỉnh A: Đỉnh A có bậc là 3, vì nó được kết nối với ba đỉnh khác là B, D và E.
3. Đường đi từ A đến E:
Đường đi 1: A -> D -> E
Đường đi 2: A -> B -> C -> D -> E
Đường đi 3: A -> E (trực tiếp vì có cạnh nối giữa chúng)
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Để vẽ và thiết lập ma trận kề của đồ thị đầy đủ với số đỉnh n=2,3,4 ta sẽ xác định tất cả các cạnh có thể nối giữa các đỉnh.
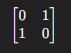
1. Khi n=2:
- Đồ thị chỉ có hai đỉnh V={0,1}
- Vì đồ thị đầy đủ, nên có một cạnh nối giữa mọi cặp đỉnh.
- Ma trận kề sẽ có dạng:
2. Khi n=3:
- Đồ thị có ba đỉnh V={0,1,2}.
- Tương tự như trường hợp trên, có một cạnh nối giữa mọi cặp đỉnh.
- Ma trận kề:
3. Khi n=4:
- Đồ thị có bốn đỉnh V={0,1,2,3}.
- Đồ thị đầy đủ có một cạnh nối giữa mọi cặp đỉnh.
- Ma trận kề:
Trong ma trận kề, giá trị 1 ở hàng i và cột j thể hiện rằng có một cạnh nối giữa đỉnh i và đỉnh j.
Lời giải
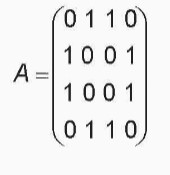
Xét từng hàng của ma trận kề:
- Hàng 1: Đỉnh 0 kề với đỉnh 1 và 2.
- Hàng 2: Đỉnh 1 kề với đỉnh 0 và 3.
- Hàng 3: Đỉnh 2 kề với đỉnh 0 và 3.
- Hàng 4: Đỉnh 3 kề với đỉnh 1 và 2.
Dựa trên thông tin này, ta có thể vẽ đồ thị như sau:
Xét từng hàng của ma trận kề:
- Hàng 1: Đỉnh 0 kề với đỉnh 1 và 2.
- Hàng 2: Đỉnh 1 kề với đỉnh 0 và 3.
- Hàng 3: Đỉnh 2 kề với đỉnh 0 và 3.
- Hàng 4: Đỉnh 3 kề với đỉnh 1 và 2.
Dựa trên thông tin này, ta có thể vẽ đồ thị như sau:
Trong đồ thị này, mỗi đỉnh được biểu diễn bởi một số, và mỗi cạnh giữa các đỉnh được biểu diễn bằng các đoạn thẳng nối hai đỉnh tương ứng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Bộ 3 đề thi cuối kì 2 Tin 12 Cánh diều có đáp án - Đề 1
-
15 câu Trắc nghiệm Tin học 12 Kết nối tri thức Bài 23 có đáp án
-
15 câu Trắc nghiệm Tin học 12 Kết nối tri thức Bài 19 có đáp án
-
Bộ 3 đề thi cuối kì 2 Tin 12 Kết nối tri thức có đáp án - Đề 1
-
15 câu Trắc nghiệm Tin học 12 Cánh diều Mô hình và các giao thức mạng có đáp án
-
15 câu Trắc nghiệm Tin học 12 Kết nối tri thức Bài 24 có đáp án
-
15 câu Trắc nghiệm Tin học 12 Kết nối tri thức Bài 25 có đáp án
-
Trắc nghiệm tổng hợp Tin học năm 2023 có đáp án (Phần 1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận