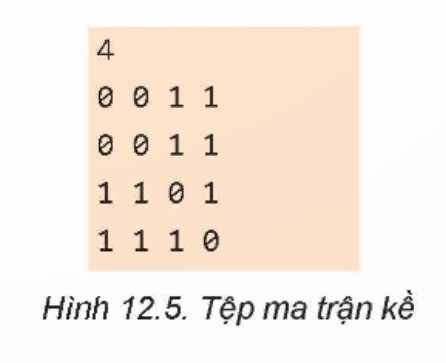
Khẳng định dãy Adj[i] có số lượng phần tử bằng số các phần tử có giá trị 1 của hàng thứ i của ma trận kề A là đúng hay sai?

Xem lời giải

Câu hỏi trong đề: Giải chuyên đề Tin 12 KNTT Bài 12: Biểu diễn đồ thị có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Khẳng định này là đúng.

Trong ma trận kề A của một đồ thị vô hướng, mỗi hàng iii tương ứng với một đỉnh, và mỗi phần tử trong hàng đó biểu diễn một cạnh nối từ đỉnh iii đến một đỉnh khác. Nếu giá trị của một phần tử là 111, nghĩa là có cạnh nối từ đỉnh iii đến đỉnh tương ứng với vị trí của phần tử đó trong hàng.

Dãy Adj[i] là danh sách kề của đỉnh iii, tức là nó chứa tất cả các đỉnh kề với đỉnh iii. Vậy nếu số lượng phần tử trong Adj[i] bằng số lượng phần tử có giá trị 1 trong hàng thứ i của ma trận kề A, điều đó có nghĩa là mỗi phần tử có giá trị 1 trong hàng thứ i của A tương ứng với một đỉnh kề của đỉnh i, và do đó, khẳng định này là đúng.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một đơn đồ thị, vô hướng có n đỉnh, có thể có số cạnh lớn nhất là bao nhiêu?

Xem đáp án

Lời giải

Trong một đơn đồ thị vô hướng có n đỉnh, số cạnh lớn nhất có thể có được là khi mỗi cặp đỉnh đều được nối với nhau bằng một cạnh. Điều này xảy ra khi đồ thị là đồ thị đầy đủ.

Một đồ thị đầy đủ có nnn đỉnh sẽ có tất cả các cặp đỉnh đều được nối với nhau bằng một cạnh.

Số cạnh của một đồ thị đầy đủ với n đỉnh được tính bằng công thức sau:

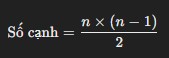
Một đơn đồ thị, vô hướng có n đỉnh, có thể có số cạnh lớn nhất là bao nhiêu? (ảnh 1)

Do mỗi cặp đỉnh được nối với nhau bằng một cạnh, và số lượng cặp đỉnh là

(lấy một đỉnh, sau đó chọn một đỉnh từ n−1 đỉnh còn lại).

Vì vậy, số cạnh lớn nhất của một đơn đồ thị vô hướng với n đỉnh là

Câu 2

Từ ma trận kề A của đồ thị G có thể tính được số các cạnh của đồ thị không? Nếu được thì tính bằng cách nào?

Xem đáp án

Lời giải

Có, từ ma trận kề A của đồ thị G, chúng ta có thể tính được số cạnh của đồ thị bằng cách đếm tổng số lượng phần tử có giá trị 1 trong ma trận kề.

Trong ma trận kề của một đồ thị vô hướng, mỗi cạnh được biểu diễn bởi một phần tử có giá trị 1. Do đó, để tính tổng số cạnh, chúng ta chỉ cần đếm tổng số lượng phần tử có giá trị 1 trong ma trận kề.

Tuy nhiên, trong một đồ thị vô hướng, mỗi cạnh thường được tính hai lần (một lần cho mỗi đỉnh mà nó kết nối). Vì vậy, sau khi đếm số lượng phần tử có giá trị 1 trong ma trận kề, chúng ta cần chia kết quả cho 2 để loại bỏ sự đếm lặp.

Do đó, cách tính số cạnh của đồ thị từ ma trận kề A như sau:

1. Đếm tổng số lượng phần tử có giá trị 1 trong ma trận kề A.

2. Chia kết quả cho 2.

Với một đồ thị vô hướng, số lượng cạnh là nửa số lượng phần tử có giá trị 1 trong ma trận kề.

Câu 3