Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông cạnh \[a,\,\,SA\] vuông góc với đáy, \({\rm{SA}} = {\rm{a}}\sqrt 2 \). Một mặt phẳng đi qua \({\rm{A}}\) vuông góc với \({\rm{SC}}\) cắt \[{\rm{SB}},\,\,{\rm{SD}},\,\,{\rm{SC}}\] lần lượt tại \(B',\,\,{\rm{D'}},\,\,C'.\) Thể tích khối chóp \({\rm{SA}}B'\,C'{\rm{D'}}\) là
Quảng cáo
Trả lời:
Giải bởi Vietjack
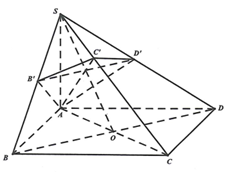
Ta có: \({V_{{\rm{S}}{\rm{.ABCD }}}} = \frac{1}{3}.{a^2}.a\sqrt 2 = \frac{{{a^3}\sqrt 2 }}{3}\).
Ta có \({\rm{AD'}} \bot \left( {{\rm{SDC}}} \right)\)
\( \Rightarrow {\rm{AD'}} \bot {\rm{SD}}\,;\,\,{\rm{A}}B' \bot \left( {{\rm{SBC}}} \right) \Rightarrow {\rm{A}}B' \bot {\rm{SB}}\).
Do \({\rm{SC}} \bot \left( {{\rm{A}}B'{\rm{D'}}} \right) \Rightarrow {\rm{SC}} \bot {\rm{A}}C'\).
Tam giác \[SAC\] vuông cân tại \(A\) nên \(C'\) là trung điểm của \[SC.\]
Trong tam giác \({\rm{SA}}B'\) ta có \(\frac{{{\rm{S}}B'}}{{{\rm{SB}}}} = \frac{{{\rm{S}}{{\rm{A}}^2}}}{{{\rm{S}}{{\rm{B}}^2}}} = \frac{{2{{\rm{a}}^2}}}{{3{{\rm{a}}^2}}} = \frac{2}{3}\).\(\frac{{{{\rm{V}}_{{\rm{SA}}B'\,C'{\rm{D'}}}}}}{{{{\rm{V}}_{{\rm{S}}.{\rm{ABCD}}}}}} = \frac{{{{\rm{V}}_{{\rm{SA}}B'\,C'}} + {{\rm{V}}_{{\rm{SA}}C'{\rm{D'}}}}}}{{{{\rm{V}}_{{\rm{S}}.{\rm{ABCD}}}}}} = \frac{1}{2}\left( {\frac{{{\rm{S}}B'}}{{{\rm{SB}}}} \cdot \frac{{{\rm{S}}C'}}{{{\rm{SC}}}} + \frac{{{\rm{SD'}}}}{{{\rm{SD}}}} \cdot \frac{{{\rm{S}}C'}}{{{\rm{SC}}}}} \right) = \frac{{{\rm{S}}B'}}{{{\rm{SB}}}} \cdot \frac{{{\rm{S}}C'}}{{{\rm{SC}}}}\)\( = \frac{2}{3} \cdot \frac{1}{2} = \frac{1}{3}\).
Vậy \({{\rm{V}}_{{\rm{SA}}B'\,C'{\rm{D'}}}} = \frac{{{{\rm{a}}^3}\sqrt 2 }}{9}\). Chọn C.
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có \(\sin x = \frac{1}{2} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{\pi }{6} + 2k\pi }\\{x = \frac{{5\pi }}{6} + 2k\pi }\end{array}(k \in \mathbb{Z})} \right.\).
Vì \(x \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) nên \(x = \frac{\pi }{6} \Rightarrow S = \frac{\pi }{6}\). Chọn D.
Lời giải
Phía bắc khu vực Mỹ La-tinh tiếp giáp với Hoa Kỳ. Chọn A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo