Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 19)
120 người thi tuần này 4.6 2.9 K lượt thi 150 câu hỏi 150 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 45)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 44)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 43)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 42)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 41)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 40)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 39)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 38)
Danh sách câu hỏi:
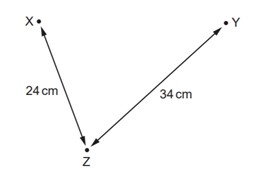
Câu 1
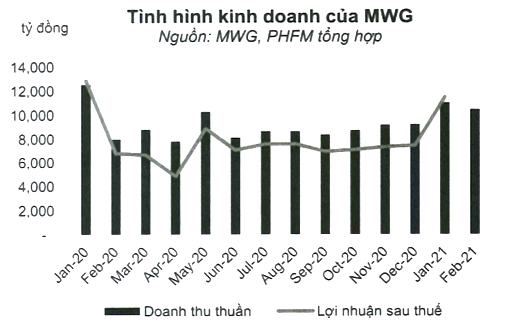
A. Từ tháng 1/2020 đến tháng 2/2020.
B. Từ tháng 12/2020 đến tháng 1/2021.
Lời giải
Câu 2
Lời giải
Ta có \(v(t) = s'(t) = 3{t^2} + 9t - 6 = 24 \Rightarrow t = 2\,\,(s);\)
\(a(t) = s''(t) = 6t + 9 \Rightarrow a(2) = 21\,\,\left( {m/{s^2}} \right)\). Chọn A.
Câu 3
Lời giải
Điều kiện xác định: \(x + 1 > 0 \Leftrightarrow x > - 1\)
\({\log _{\frac{1}{2}}}\left( {x + 1} \right) > - 2 \Leftrightarrow - {\log _2}\left( {x + 1} \right) > - 2 \Leftrightarrow {\log _2}\left( {x + 1} \right) < 2 \Leftrightarrow 0 < x + 1 < 4 \Leftrightarrow - 1 < x < 3\)
Vậy tập nghiệm của bất phương trình là \(S = \left( { - 1\,;\,\,3} \right)\). Chọn B.
Lời giải
Khi \(x,\,\,y \ge 0\) thì hệ trở thành \(\left\{ {\begin{array}{*{20}{l}}{x + 2y = 3}\\{7x + 5y = 2}\end{array} \Leftrightarrow x = - \frac{{11}}{9};y = \frac{{19}}{9}} \right.\) (loại)
• Khi \(x,y < 0\) thì hệ trở thành \(\left\{ {\begin{array}{*{20}{l}}{ - x - 2y = 3}\\{7x + 5y = 2}\end{array} \Leftrightarrow x = \frac{{19}}{9};\,\,y = \frac{{ - 23}}{9}} \right.\) (loại).
• Khi \(x \ge 0,\,\,y < 0\) thì hệ trở thành \(\left\{ {\begin{array}{*{20}{l}}{x - 2y = 3}\\{7x + 5y = 2}\end{array} \Leftrightarrow x = 1;\,\,y = - 1} \right.\) (nhận).
• Khi \(x < 0,\,\,y \ge 0\) thì hệ trở thành \(\left\{ {\begin{array}{*{20}{l}}{ - x + 2y = 3}\\{7x + 5y = 2}\end{array} \Leftrightarrow x = - \frac{{11}}{{19}};\,\,y = \frac{{23}}{{19}}} \right.\) (nhận). Chọn C.
Câu 5
Lời giải
Xét \(\Delta = {2^2} - 4 \cdot 1 \cdot 10 = - 36 < 0\) suy ra phương trình \({{\rm{z}}^2} + 2{\rm{z}} + 10 = 0\) có hai nghiệm phức là \[{z_1} = - 1 - 3i\,;\,\,{z_2} = - 1 + 3i\].
Theo đề bài ta có \({{\rm{z}}_0}\) là nghiệm phức có phần thực âm và phần ảo dương của phương trình \({{\rm{z}}^2} + 2{\rm{z}} + 10 = 0\) nên \({{\rm{z}}_0} = - 1 + 3{\rm{i}} \Rightarrow {\rm{i}}{{\rm{z}}_0} = {\rm{i}}\left( { - 1 + 3{\rm{i}}} \right) = - 3 - {\rm{i}}\).
Vậy điểm \({\rm{M}}\left( { - 3\,;\,\, - 1} \right)\) là điểm biểu diễn số phức \({\rm{w}} = {\rm{i}}{{\rm{z}}_0} = - 3 - {\rm{i}}\). Chọn D.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
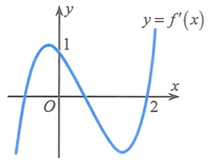
A. \(m \le f\left( 2 \right) - 2\).
B. \(m < f\left( 2 \right) - 2\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
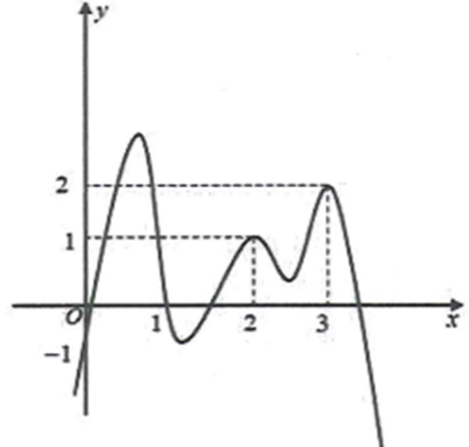
A. \(\left( { - \infty \,;\,\,0} \right] \cup \left[ {3\,;\,\, + \infty } \right)\).
B. \(\left[ {0\,;\,\,2} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
A. \(\frac{{16\pi }}{3}\).
B. \(\frac{{32\pi }}{3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
A. Một đường thẳng.
B. Đường tròn có bán kính \({\rm{R}} = \frac{1}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
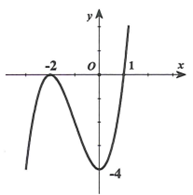
A. \(\left( {0\,;\,\,0} \right)\) và \(\left( {0\,;\,\,\frac{4}{3}} \right)\).
B. \(\left( {1\,;\,\,0} \right)\) và \(\left( {0\,;\,\,\frac{4}{3}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
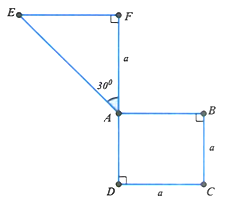
A. \(\frac{{5\pi }}{2}{{\rm{a}}^3}\).
B. \(\frac{{10\pi }}{7}{{\rm{a}}^3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 25
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 26
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 27
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 28
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 30
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 32
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 33
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 34
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 35
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 51
A. trong.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 52
A. từ ghép.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 53
A. quan điểm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 54
A. được.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 55
A. ý tưởng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 56
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 57
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 58
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 59
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 60
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 61
A. sinh thái.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 63
A. không những/ mà còn.
B. vì/ nên.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 64
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 65
A. hùng ca – tình ca.
B. đồng ca – anh hùng ca.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 66
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 67
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 68
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 70
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 72
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 73
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 74
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 75
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 78
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 79
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 80
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 81
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 82
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 83
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 84
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 85
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 86
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 87
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 88
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 89
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 90
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 91
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 92
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 93
A. Tốc độ tăng trưởng số trang trại phân theo lĩnh vực hoạt động của nước ta năm 2011 và 2021.
B. Số lượng trang trại phân theo lĩnh vực hoạt động của nước ta năm 2011 và 2021.
C. Sự chuyển dịch cơ cấu trang trại phân theo lĩnh vực hoạt động của nước ta năm 2011 và 2021.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 94
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 95
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 96
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 97
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 98
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 100
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 102
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 103
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 104
A. 2 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 105
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 106
A. 4,8.10-23 W/m2
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 108
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 109
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 110
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 111
A. 45,92 lít.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 112
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 113
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 114
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 116
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 118
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 119
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 120
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 121
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 123
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 125
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 126
A. Quần thể I.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 1
Đọc đoạn trích sau và trả lời các câu hỏi từ 51 đến 55:
Đọc, trong nghĩa đó là một trò chơi. Nơi mỗi người đọc có ba nhân vật chồng lên nhau, tác động lên nhau. Một là người đọc bằng xương bằng thịt, hai chân đụng đất, vẫn còn ý thức liên hệ với thế giới bên ngoài. Hai là, người đọc bị lôi cuốn, đang ngao du trong thế giới tưởng tượng của cảm xúc. Đó là người đang chơi. Ba là, người đọc suy tư, đưa vào trò chơi sự chú ý, sự suy nghĩ, sự phán đoán của tri thức. Đó là phút giây của trí tuệ có khả năng đưa người đọc lùi ra khỏi bài văn, mở một khoảng cách để diễn dịch. Người đọc vẫn ý thức rằng mình đang chơi nhưng biết phán đoán. Ba tay chơi là một trong việc đọc, chơi với nhau một trò chơi tinh tế khiến người đọc vừa bị lôi cuốn vừa biết dừng lại, vừa tham dự vừa cách biệt với bài văn. Tư thế của người đọc văn là vậy: tham dự và cách biệt qua lại không đứt quãng.
(Trích “Chuyện trò” – Cao Huy Thuần, NXB Trẻ, 2013)
Câu 128
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 130
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 131
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 132
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 2
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 56 đến 60:
... Hắn bâng khuâng như tỉnh dậy, hắn thấy miệng đắng, lòng mơ hồ buồn. Người thì bủn rủn, chân tay không buồn nhấc, hay là đói rượu, hắn hơi rùng mình. Ruột gan lại nôn nao lên một tí. Hắn sợ rượu cũng như những người ốm sợ cơm. Tiếng chim hót ngoài kia vui vẻ quá! Có tiếng cười nói của những người đi chợ. Anh thuyền chài gõ mái chèo đuổi cá.
Những tiếng quen thuộc ấy hôm nào chả có. Nhưng hôm nay hắn mới nghe thấy... Chao ôi là buồn!
....Hắn nôn nao buồn, là vì mẩu chuyện ấy nhắc cho hắn một cái gì rất xa xôi. Hình như có một thời hắn đã ao ước có một gia đình nho nhỏ. Chồng cuốc mướn cày thuê, vợ dệt vải, chúng lại bỏ một con lợn nuôi để làm vốn liếng. Khá giả thì mua dăm ba sào ruộng làm.
(Chí Phèo – Nam Cao)
Câu 133
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 134
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 135
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 136
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 137
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 61 đến 65:
(1) Hôm nay, trời nhẹ lên cao,
(2) Tôi buồn không hiểu vì sao tôi buồn...
(3) Lá hồng rơi lặng ngõ thuôn,
(4) Sương trinh rơi kín từ nguồn yêu thương.
(5) Phất phơ hồn của bông hường,
(6) Trong hơi phiêu bạt còn vương máu hồng.
(7) Nghe chừng gió nhớ qua sông,
(8) E bên lau lách thuyền không vắng bờ.
(9) Không gian như có dây tơ,
(10) Bước đi sẽ đứt, động hờ sẽ tiêu.
(11) Êm êm chiều ngẩn ngơ chiều,
(12) Lòng không sao cả, hiu hiu khẽ buồn...
(Xuân Diệu, Chiều, Tuyển tập Tự lực văn đoàn (tập III), NXB Hội Nhà văn, 2004)
Câu 138
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 139
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 140
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 141
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 142
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 66 đến 70:
(1) Tất cả các sinh vật sống đều có những đặc điểm riêng biệt, nhưng mọi thứ ở loài hải sâm đều khác thường. Có thể nói đây là loài động vật kì dị nhất trong số những loài động vật kì dị.
(2) Nơi sống chủ yếu của hải sâm là vùng nước nông, có nhiều cát hoặc trên bề mặt của các bãi bùn. Thức ăn chính của chúng là bùn, tảo, ốc và các chất hữu cơ dưới biển. Một trong những cách chúng bắt mồi là nằm trong làn nước và bắt những loài phù du trôi trong đó bằng các xúc tu. Hải sâm rất phàm ăn, chúng kiếm ăn gần như liên tục cả ngày lẫn đêm nhưng lại có thể sống mà không cần ăn trong thời gian dài. Khác với nhiều loài sinh vật khác ngủ đông, sâm biển thường ngủ hè bởi cơ thể của chúng rất nhạy với sự thay đổi nhiệt độ của nước biển, khả năng chịu nóng kém. Với đặc điểm đó, vào mùa hè, sâm biển thường nằm im dưới đáy biển và hầu như không ăn uống, bơi lội. Chúng sẽ xuất hiện trở lại khi thời tiết chuyển sang thu. Trong khoảng thời gian đó, sự trao đổi chất của chúng diễn ra rất chậm. Vì thế mà các sinh vật phù du có thời gian sinh sôi và phát triển. Nếu không, với sức ăn của chúng, nguồn thức ăn sẽ nhanh chóng cạn kiệt và chúng sẽ bị chết đói.
(3) Hải sâm có nhiều màu sắc khác nhau, từ đen đến nâu đỏ đến màu cát và gần như trắng, có loại còn có xúc tu màu tím sặc sỡ. Tên tiếng Anh của loài này là Sea cucumber, nghĩa là dưa chuột biển do thân hình của loài vật này giống quả dưa chuột. Hình dáng đặc biệt kết hợp với sự mềm dẻo, linh hoạt của cơ thể cho phép chúng dễ dàng len lỏi vào các khe đá, ở đó chúng được an toàn trước những kẻ săn mồi và dòng chảy của đại dương.
(4) Nhắc đến hải sâm chúng ta đều nghĩ chúng là loài động vật khá nhàm chán. Tuy nhiên khi phải đối mặt với sự sống còn thì mọi thứ lại trở nên thú vị. Giống như sao biển và nhím biển, hải sâm là động vật da gai và chúng có thể tự tái tạo bộ phận cơ thể bị mất nếu cần thiết. Hải sâm sẽ tự đào thải và tự tái sinh khi bị dính vào một thứ gì đó hoặc bị vật khác chạm vào; nó cũng sẽ làm như vậy nếu nhiệt độ nước xung quanh quá cao hoặc nguồn nước trở nên quá ô nhiễm. Khi bị đe dọa, những con hải sâm sẽ phun tất cả các cơ quan nội tạng của mình xuống nước, những thứ này chứa một hóa chất độc hại có thể giết chết kẻ thù.
(Sưu tầm)
Câu 143
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 144
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 145
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 146
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 147
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 5
Dựa vào các thông tin sau đây để trả lời các câu hỏi từ câu 108 đến câu 110:
"Tư sản Việt Nam đã tố chức cuộc tẩy chay tư sản Hoa kiều, vận động người Việt Nam chỉ mua hàng của người Việt Nam, "chấn hưng nội hoá", "bài trừ ngoại hoá".
Năm 1923, địa chủ và tư sản Việt Nam đấu tranh chống độc quyền cảng Sài Gòn, độc quyền xuất cảng lúa gạo tại Nam Kì của tư bản Pháp.
Một số tư sản và địa chủ lớn ở Nam Kì (đại biểu là Bùi Quang Chiêu, Nguyễn Phan Long v.v.) lập ra Đảng Lập hiến (1923). Đảng này đưa ra một số khẩu hiệu đòi tự do, dân chủ. Nhưng khi được thực dân Pháp nhượng bộ một số quyền lợi (như cho tham gia Hội đồng Quản hạt Nam Ki), họ lại thỏa hiệp với chúng. Ngoài Đảng Lập hiến, còn có nhóm Nam Phong của Phạm Quỳnh cổ vũ thuyết "quân chủ lập hiến", nhóm Trung Bắc tân văn của Nguyễn Văn Vĩnh đề cao tư tưởng "trực trị".
Tâng lớp tiểu tư sản trí thức (gồm sinh viên, học sinh và giáo viên, viên chức, nhà văn, nhà báo v.v.) sôi nổi đấu tranh đòi những quyền tự do, dân chủ. Một số tổ chức chính trị như Việt Nam nghĩa đoàn, Hội Phục Việt, Đảng Thanh niên (đại biểu là Tôn Quang Phiệt, Đặng Thai Mai, Trần Huy Liệu, Nguyễn An Ninh v.v.) được thành lập với nhiều hoạt động phong phú và sôi động (mít tinh, biểu tình, bãi khóa v.v.). Nhiều tờ báo tiến bộ lần lượt ra đời. Báo tiếng Pháp có các tờ Chuông rè, An Nam trẻ, Người nhà quê. Báo tiếng Việt có Hữu thanh, Tiếng dân, Đông Pháp thời báo, Thực nghiệp dân báo.... Một số nhà xuất bản tiến bộ như Nam đồng thư xã (Hà Nội), Cường học thư xã (Sài Gòn), Quan hải tùng thư (Huế) v.v. đã phát hành nhiều loại sách báo tiến bộ".
(Nguồn: SGK Lịch sử 12, NXB Giáo dục Việt Nam, 2023, trang 80)
Câu 148
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 149
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 150
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

![Một máy bơm sử dụng cho đài phun nước được nối bởi dây dẫn cách nguồn điện 18 m. Nguồn điện có hiệu điện thế hiệu dụng 230 V. Máy bơm hoạt động bình thường với điện áp hiệu dụng thấp nhất là 218 V và cường độ dòng điện 0,83 A. Điện trở lớn nhất trên mỗi mét chiều dài dây dẫn là bao nhiêu để máy bơm hoạt động bình thường? A. \[0,4\,\Omega /m.\] B. \[0,8\,\Omega /m.\] C. \[1,3\,\Omega /m.\] D. \[1,4\,\Omega /m.\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/07/blobid13-1721867001.png)