Câu hỏi:
12/07/2024 671
Đọc đoạn văn sau và trả lời câu hỏi từ 21 - 26
Các nhà nghiên cứu đã tiến hành thử nghiệm trên một đơn thuốc nhất định, thuốc được phân phối dưới dạng viên nang giải phóng tức thời và viên nang giải phóng kéo dài.
Viên nang giải phóng tức thời (immediate-release) được bào chế nhằm phóng thích nhanh và hoàn toàn hoạt chất ngay sau khi uống hoặc viên được hòa tan, dùng như dung dịch thuốc. Viên nang giải phóng kéo dài (extended-release), hoạt chất không được phóng thích ngay sau khi dùng mà cần một thời gian nhất định hoặc điều kiện phù hợp đến trễ hơn.
Hình 1 cho thấy nồng độ trung bình (nanogram trên mililit [ng/mL]) của hai hoạt chất của thuốc theo toa trong huyết tương của bệnh nhân theo thời gian (giờ).
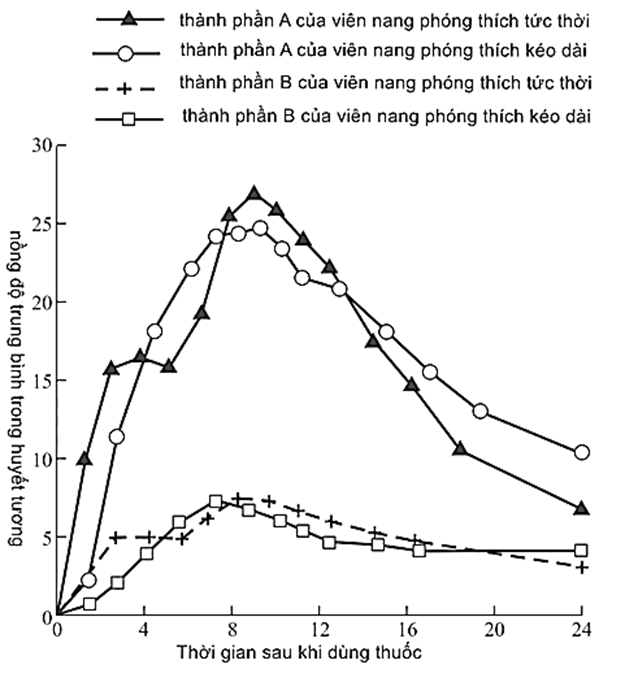
Hình 1. Mean blood pressure concentrantion (nồng độ trung bình trong huyết tương).
Trong các thử nghiệm lâm sàng về thuốc theo toa, các đối tượng được cho thuốc theo toa đã được phỏng vấn đều đặn về các triệu chứng sau khi dùng. Sau mỗi cuộc phỏng vấn, các đối tượng được chỉ định một triệu chứng. Điểm số triệu chứng cao tương ứng với cường độ cao của triệu chứng và điểm triệu chứng thấp cho thấy cường độ thấp của các triệu chứng. Hình 2 cho thấy điểm triệu chứng trung bình trên thời gian (giờ) đối với đối tượng dùng thuốc theo đơn.
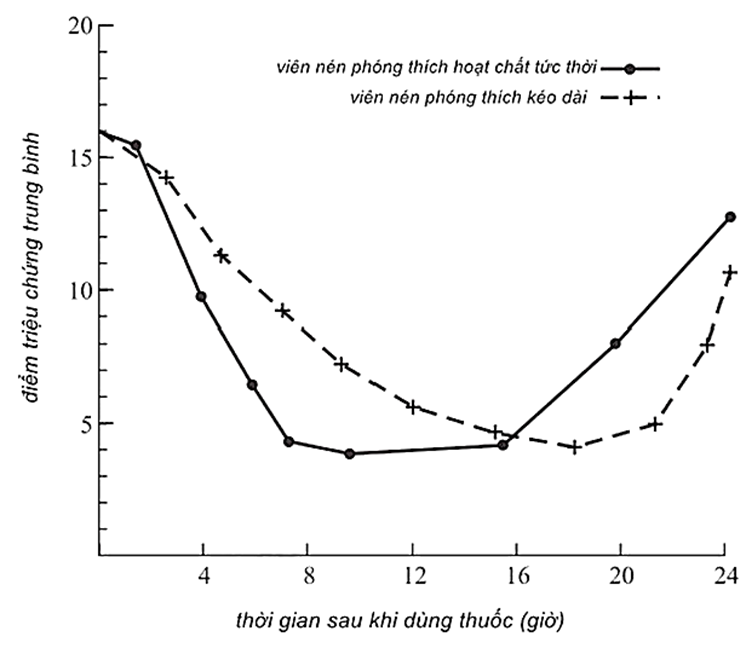
Hình 2. Mean symptom score (điểm triệu chứng trung bình)
Phần tư duy khoa học/ giải quyết vấn đề
Điền đáp án chính xác vào chỗ trống
Theo hình 1, 16 giờ sau khi dùng dạng viên nén giải phóng kéo dài của thuốc theo toa, sự chênh lệch về nồng độ trung bình giữa thành phần A và thành phần B trong huyết tương gần nhất với _________ ng/ml
Đọc đoạn văn sau và trả lời câu hỏi từ 21 - 26
Các nhà nghiên cứu đã tiến hành thử nghiệm trên một đơn thuốc nhất định, thuốc được phân phối dưới dạng viên nang giải phóng tức thời và viên nang giải phóng kéo dài.
Viên nang giải phóng tức thời (immediate-release) được bào chế nhằm phóng thích nhanh và hoàn toàn hoạt chất ngay sau khi uống hoặc viên được hòa tan, dùng như dung dịch thuốc. Viên nang giải phóng kéo dài (extended-release), hoạt chất không được phóng thích ngay sau khi dùng mà cần một thời gian nhất định hoặc điều kiện phù hợp đến trễ hơn.
Hình 1 cho thấy nồng độ trung bình (nanogram trên mililit [ng/mL]) của hai hoạt chất của thuốc theo toa trong huyết tương của bệnh nhân theo thời gian (giờ).
Hình 1. Mean blood pressure concentrantion (nồng độ trung bình trong huyết tương).
Trong các thử nghiệm lâm sàng về thuốc theo toa, các đối tượng được cho thuốc theo toa đã được phỏng vấn đều đặn về các triệu chứng sau khi dùng. Sau mỗi cuộc phỏng vấn, các đối tượng được chỉ định một triệu chứng. Điểm số triệu chứng cao tương ứng với cường độ cao của triệu chứng và điểm triệu chứng thấp cho thấy cường độ thấp của các triệu chứng. Hình 2 cho thấy điểm triệu chứng trung bình trên thời gian (giờ) đối với đối tượng dùng thuốc theo đơn.
Hình 2. Mean symptom score (điểm triệu chứng trung bình)
Phần tư duy khoa học/ giải quyết vấn đề
Điền đáp án chính xác vào chỗ trống
Theo hình 1, 16 giờ sau khi dùng dạng viên nén giải phóng kéo dài của thuốc theo toa, sự chênh lệch về nồng độ trung bình giữa thành phần A và thành phần B trong huyết tương gần nhất với _________ ng/ml
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án: “11”
Phương pháp giải
Dựa vào thông tin hình 1
Lời giải
Đáp án là 11 ng/ml
Theo hình 1, 16 giờ sau khi dùng dạng viên nén giải phóng kéo dài của thuốc theo toa có nồng độ trung bình thành phần A trong huyết tương khoảng 15 ng/ml và nồng độ trung bình thành phần B trong huyết tương khoảng 4 ng/ml => Sự khác biệt về nồng độ trung bình trong huyết tương giữa thành phần A và thành phần B gần nhất với 11 ng/ml
Câu hỏi cùng đoạn
Câu 2:
Dựa trên dữ liệu trong hình 1 và hình 2, nhận định nào sau đây phù hợp nhất về nồng độ trung bình trong huyết tương và điểm số triệu chứng trung bình theo thời gian sau khi dùng thuốc?
Dựa trên dữ liệu trong hình 1 và hình 2, nhận định nào sau đây phù hợp nhất về nồng độ trung bình trong huyết tương và điểm số triệu chứng trung bình theo thời gian sau khi dùng thuốc?
Lời giải của GV VietJack
Phương pháp giải
Kết hợp xem hình 1 và hình 2
Lời giải
Theo hình 2, phải mất 1 khoảng thời gian để thuốc bắt đầu phát huy tác dụng, sau đó thuốc phát huy tác dụng, các triệu chứng giảm đi trong 1 khoảng thời gian, sau đó các triệu chứng trở lại (có thể là thuốc bắt đầu trơ đi và mất tác dụng)
Hơn nữa, theo hình 1 cho thấy sự thuyên giảm triệu chứng tỉ lệ nghịch với nồng độ thuốc trong cơ thể
=> Nồng độ trung bình trong huyết tương tăng sau đó giảm và điểm số triệu chứng trung bình giảm sau đó tăng.
=> Chọn C
Câu 3:
Theo hình 1, nồng độ trung bình trong huyết tương của thành phần A được sử dụng ở dạng phóng thích tức thời tăng nhiều nhất trong khoảng thời gian nào?
Theo hình 1, nồng độ trung bình trong huyết tương của thành phần A được sử dụng ở dạng phóng thích tức thời tăng nhiều nhất trong khoảng thời gian nào?
Lời giải của GV VietJack
Phương pháp giải
Dựa vào hình 1
Lời giải
Theo hình 1, nồng độ trung bình trong huyết tương của thành phần A được sử dụng ở dạng phóng thích tức thời tăng nhiều nhất là khoảng thời gian ngay sau sử dụng thuốc đến 4 giờ sau khi dùng thuốc.
Câu 4:
Nhận định nào sau đây đúng hay sai
Nồng độ trong huyết tương trung bình của thành phần B được sử dụng dưới dạng viên nang phóng thích tức thời luôn thấp hơn nồng độ trong huyết tương trung bình của thành phần A trong khoảng 24 giờ sau khi dùng thuốc, đúng hay sai?
Nhận định nào sau đây đúng hay sai
Nồng độ trong huyết tương trung bình của thành phần B được sử dụng dưới dạng viên nang phóng thích tức thời luôn thấp hơn nồng độ trong huyết tương trung bình của thành phần A trong khoảng 24 giờ sau khi dùng thuốc, đúng hay sai?
Lời giải của GV VietJack
Phương pháp giải
Dựa vào hình 1
Lời giải
Theo hình 1, nồng độ trong huyết tương trung bình của thành phần B được sử dụng dưới dạng viên nang phóng thích hoạt chất tức luôn thấp hơn nồng độ trong huyết tương trung bình của thành phần A trong khoảng 24 giờ sau khi dùng thuốc
=> Chọn A
Câu 5:
Điểm triệu chứng của một đối tượng thử nghiệm lâm sàng được dùng viên nang dạng giải phóng kéo dài của thuốc theo toa không thay đổi trong 8 giờ. Dựa vào bảng 2, khoảng thời gian đó rất có thể bắt đầu sau bao lâu sử dụng thuốc?
Điểm triệu chứng của một đối tượng thử nghiệm lâm sàng được dùng viên nang dạng giải phóng kéo dài của thuốc theo toa không thay đổi trong 8 giờ. Dựa vào bảng 2, khoảng thời gian đó rất có thể bắt đầu sau bao lâu sử dụng thuốc?
Lời giải của GV VietJack
Phương pháp giải
Dựa vào bảng 2
Lời giải
Dựa vào hình 2, ta dễ dàng nhận thấy khoảng thời gian sau 14 giờ sử dụng đến 22 giờ sau sử dụng có đường cong với độ dốc thay đổi ít nhất
=> Điểm triệu chứng của một đối tượng thử nghiệm lâm sàng được dùng viên nang dạng giải phóng kéo dài của thuốc theo toa không thay đổi trong khoảng thời gian này.
=> Chọn D
Câu 6:
Giả sử thành phần A có tác dụng phụ là làm người sử dụng có cảm giác buồn nôn và chỉ có tác dụng khi đạt nồng độ trong huyết tương trung bình trên 25 ng/ml. Một người sử dụng thuốc có chứa viên nén nêu trên, nhận định nào sau đây chính xác?
Giả sử thành phần A có tác dụng phụ là làm người sử dụng có cảm giác buồn nôn và chỉ có tác dụng khi đạt nồng độ trong huyết tương trung bình trên 25 ng/ml. Một người sử dụng thuốc có chứa viên nén nêu trên, nhận định nào sau đây chính xác?
Lời giải của GV VietJack
Phương pháp giải
Dựa vào bảng 1
Lời giải
Vì sau khoảng 8 giờ nồng độ trong huyết tương trung bình của thành phần A đạt khoảng 25 ng/ml, và sau khoảng 10 giờ sẽ giảm xuống dưới mức 25 ng/ml
=> Người sử dụng viên nén nêu trên sau khoảng 8 giờ sử dụng sẽ cảm thấy buồn nôn và hết sau khoảng 10 giờ.
=> Chọn D
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: “28”
Phương pháp giải
Vì S là tập hợp tất cả các số tự nhiên có ít nhất 3 chữ số, các chữ số đôi một khác nhau được lập thành từ các chữ số thuộc tập A
Lời giải
Vì S là tập hợp tất cả các số tự nhiên có ít nhất 3 chữ số, các chữ số đôi một khác nhau được lập thành từ các chữ số thuộc tập A nên ta tính số phần tử thuộc tập Snhư sau:
+ Số các số thuộc S có 3 chữ số là \(A_5^3\).
+ Số các số thuộc S có 4 chữ số là \(A_5^4\).
+ Số các số thuộc S có 5 chữ số là \(A_5^5\).
Suy ra số phần tử của tập S là \(A_5^3 + A_5^4 + A_5^5 = 300.\)
Số phần tử của không gian mẫu là \({n_\Omega } = C_{300}^1 = 300\)
Gọi X là biến cố “Số được chọn có tổng các chữ số bằng 10”. Các tập con của A có tổng số phần tử bằng 10 là A1 = {1;2;3;4}, A2 = {2;3;5}, A3 = {1;4;5}.
+ Từ A1 lập được các số thuộc S là 4!.
+ Từ A2 lập được các số thuộc S là 3!.
+ Từ A3 lập được các số thuộc S là 3!.
Suy ra số phần tử của biến cố X là nX = 4! + 3! + 3! = 36.
Vậy xác suất cần tính \(P(X) = \frac{{{n_X}}}{{{n_\Omega }}} = \frac{{36}}{{300}} = \frac{3}{{25}}.\)
Lời giải
Phương pháp giải
Dạng vô định ∞ - ∞
Lời giải
Ta có \(\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {a{x^2} + 1} - bx - 2}}{{{x^3} - 3x + 2}} = \mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {a{x^2} + 1} - bx - 2}}{{{{(x - 1)}^2}(x + 2)}} = L,\) với \(L \in \mathbb{R}\)(*)
Khi đó \(\sqrt {a + 1} - b - 2 = 0 \Leftrightarrow \sqrt {a + 1} = b + 2 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{b \ge - 2}\\{a + 1 = {b^2} + 4b + 4}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{b \ge - 2}\\{a = {b^2} + 4b + 3}\end{array}} \right.\)
Thay \(a = {b^2} + 4b + 3\) vào (*):
\(\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {a{x^2} + 1} - bx - 2}}{{{x^3} - 3x + 2}} = \mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {\left( {{b^2} + 4b + 3} \right){x^2} + 1} - bx - 2}}{{{{(x - 1)}^2}(x + 2)}}\)
\( = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {{b^2} + 4b + 3} \right){x^2} + 1 - {{(bx + 2)}^2}}}{{{{(x - 1)}^2}(x + 2)\left[ {\sqrt {\left( {{b^2} + 4b + 3} \right){x^2} + 1} + bx + 2} \right]}}\)
\( = \mathop {\lim }\limits_{x \to 1} \frac{{(4b + 3){x^2} - 4bx - 3}}{{{{(x - 1)}^2}(x + 2)\left[ {\sqrt {\left( {{b^2} + 4b + 3} \right){x^2} + 1} + bx + 2} \right]}}\)
\( = \mathop {\lim }\limits_{x \to 1} \frac{{(4b + 3)x + 3}}{{(x - 1)(x + 2)\left[ {\sqrt {\left( {{b^2} + 4b + 3} \right){x^2} + 1} + bx + 2} \right]}} = L,\,\,L \in \mathbb{R}\)
Khi đó: \((4b + 3) + 3 = 0 \Leftrightarrow b = - \frac{3}{2} \Rightarrow a = - \frac{3}{4}.\)
Vậy \({a^2} + {b^2} = \frac{{45}}{{16}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 1)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 24)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 2)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 18)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 29)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 6)
-
ĐGTD ĐH Bách khoa - Tư duy Toán học - Xác suất của biến cố và các quy tắc tính xác suất
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 4)