Câu hỏi:
12/07/2024 344
Đọc đoạn văn sau và trả lời câu hỏi từ 27 - 29
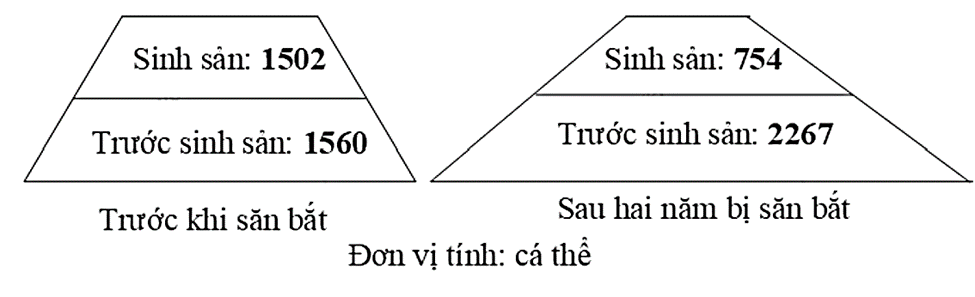
Cấu trúc tuổi của quần thể có tính đặc trưng và phụ thuộc vào môi trường sống. Khi điều tra quần thể chim trĩ (Phasianus colchicus) tại các khu rừng trên đảo Ha-oai sau hai năm bị săn bắt, người ta thu được tháp tuổi như hình dưới.
Điền đáp án chính xác vào chỗ trống
Phần trăm cá thể ở lứa tuổi trước sinh sản của quần thể trước khi bị săn bắt là: _________%
Đọc đoạn văn sau và trả lời câu hỏi từ 27 - 29
Cấu trúc tuổi của quần thể có tính đặc trưng và phụ thuộc vào môi trường sống. Khi điều tra quần thể chim trĩ (Phasianus colchicus) tại các khu rừng trên đảo Ha-oai sau hai năm bị săn bắt, người ta thu được tháp tuổi như hình dưới.
Điền đáp án chính xác vào chỗ trống
Phần trăm cá thể ở lứa tuổi trước sinh sản của quần thể trước khi bị săn bắt là: _________%
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án: “51”
Phương pháp giải
Dựa vào kết quả điều tra
Lời giải
Trước và sau khi bị săn bắt đều không thấy xuất hiện nhóm tuổi sau sinh sản. Trước khi bị săn bắt, quần thể có 51% cá thể ở lứa tuổi trước sinh sản, 49% cá thể ở lứa tuổi sinh sản => Đặc điểm đặc trưng của loài
=> 51%
Câu hỏi cùng đoạn
Câu 2:
Nhận xét nào đúng về kích thước quần thể sau 2 năm bị khai thác?
Nhận xét nào đúng về kích thước quần thể sau 2 năm bị khai thác?
Lời giải của GV VietJack
Phương pháp giải
Dựa vào kết quả điều tra
Lời giải
Sau hai năm bị săn bắt, số cá thể ở lứa tuổi sinh sản giảm mạnh => chủ yếu khai thác nhóm tuổi trưởng thành => Tỷ lệ nhóm tuổi thay đổi, quần thể có 75% cá thể ở lứa tuổi trước sinh sản, 25% cá thể ở lứa tuổi sinh sản.
Kích thước quần thể ít biến động (trước khai thác: 3062, sau hai năm khai thác: 3021)
=> việc khai thác nằm trong khả năng tự phục hồi của quần thể
=> Chọn C
Câu 3:
Nếu việc săn bắt dừng lại, thành phần nhóm tuổi của quần thể sẽ như thế nào? Biết khi dừng khai thác thì mật độ quần thể tăng lên?
Nếu việc săn bắt dừng lại, thành phần nhóm tuổi của quần thể sẽ như thế nào? Biết khi dừng khai thác thì mật độ quần thể tăng lên?
Lời giải của GV VietJack
Phương pháp giải
Dựa vào kết quả điều tra
Lời giải
Khi dừng khai thác, mật độ quần thể tăng => quần thể tự điều chỉnh, giảm khả năng sinh sản của các cá thể => số lượng cá thể giảm => quần thể quay lại tỷ lệ nhóm tuổi ban đầu
=> Chọn C
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: “28”
Phương pháp giải
Vì S là tập hợp tất cả các số tự nhiên có ít nhất 3 chữ số, các chữ số đôi một khác nhau được lập thành từ các chữ số thuộc tập A
Lời giải
Vì S là tập hợp tất cả các số tự nhiên có ít nhất 3 chữ số, các chữ số đôi một khác nhau được lập thành từ các chữ số thuộc tập A nên ta tính số phần tử thuộc tập Snhư sau:
+ Số các số thuộc S có 3 chữ số là \(A_5^3\).
+ Số các số thuộc S có 4 chữ số là \(A_5^4\).
+ Số các số thuộc S có 5 chữ số là \(A_5^5\).
Suy ra số phần tử của tập S là \(A_5^3 + A_5^4 + A_5^5 = 300.\)
Số phần tử của không gian mẫu là \({n_\Omega } = C_{300}^1 = 300\)
Gọi X là biến cố “Số được chọn có tổng các chữ số bằng 10”. Các tập con của A có tổng số phần tử bằng 10 là A1 = {1;2;3;4}, A2 = {2;3;5}, A3 = {1;4;5}.
+ Từ A1 lập được các số thuộc S là 4!.
+ Từ A2 lập được các số thuộc S là 3!.
+ Từ A3 lập được các số thuộc S là 3!.
Suy ra số phần tử của biến cố X là nX = 4! + 3! + 3! = 36.
Vậy xác suất cần tính \(P(X) = \frac{{{n_X}}}{{{n_\Omega }}} = \frac{{36}}{{300}} = \frac{3}{{25}}.\)
Lời giải
Phương pháp giải
Dạng vô định ∞ - ∞
Lời giải
Ta có \(\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {a{x^2} + 1} - bx - 2}}{{{x^3} - 3x + 2}} = \mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {a{x^2} + 1} - bx - 2}}{{{{(x - 1)}^2}(x + 2)}} = L,\) với \(L \in \mathbb{R}\)(*)
Khi đó \(\sqrt {a + 1} - b - 2 = 0 \Leftrightarrow \sqrt {a + 1} = b + 2 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{b \ge - 2}\\{a + 1 = {b^2} + 4b + 4}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{b \ge - 2}\\{a = {b^2} + 4b + 3}\end{array}} \right.\)
Thay \(a = {b^2} + 4b + 3\) vào (*):
\(\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {a{x^2} + 1} - bx - 2}}{{{x^3} - 3x + 2}} = \mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {\left( {{b^2} + 4b + 3} \right){x^2} + 1} - bx - 2}}{{{{(x - 1)}^2}(x + 2)}}\)
\( = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {{b^2} + 4b + 3} \right){x^2} + 1 - {{(bx + 2)}^2}}}{{{{(x - 1)}^2}(x + 2)\left[ {\sqrt {\left( {{b^2} + 4b + 3} \right){x^2} + 1} + bx + 2} \right]}}\)
\( = \mathop {\lim }\limits_{x \to 1} \frac{{(4b + 3){x^2} - 4bx - 3}}{{{{(x - 1)}^2}(x + 2)\left[ {\sqrt {\left( {{b^2} + 4b + 3} \right){x^2} + 1} + bx + 2} \right]}}\)
\( = \mathop {\lim }\limits_{x \to 1} \frac{{(4b + 3)x + 3}}{{(x - 1)(x + 2)\left[ {\sqrt {\left( {{b^2} + 4b + 3} \right){x^2} + 1} + bx + 2} \right]}} = L,\,\,L \in \mathbb{R}\)
Khi đó: \((4b + 3) + 3 = 0 \Leftrightarrow b = - \frac{3}{2} \Rightarrow a = - \frac{3}{4}.\)
Vậy \({a^2} + {b^2} = \frac{{45}}{{16}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 1)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 24)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 2)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 18)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 29)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 6)
-
ĐGTD ĐH Bách khoa - Tư duy Toán học - Xác suất của biến cố và các quy tắc tính xác suất
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 4)