Tứ giác MNPQ ở Hình 4a gồm 4 đỉnh M, N, P, Q và 4 cạnh MN, NP, PQ, QM. Ngũ giác ABCDE ở Hình 4b gồm 5 đỉnh A, B, C, D, E và 5 cạnh AB, BC, CD, DE, EA.
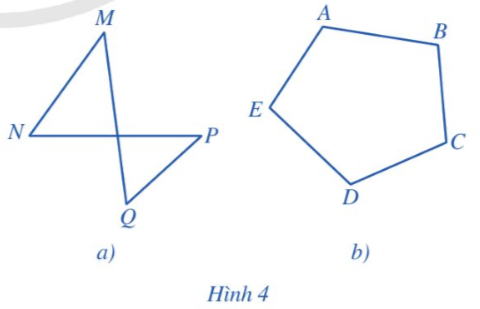
Quan sát hai hình đó, hãy cho biết các phát biểu sau là đúng hay sai:
Mỗi đỉnh là điểm chung của đúng hai cạnh
Tứ giác MNPQ ở Hình 4a gồm 4 đỉnh M, N, P, Q và 4 cạnh MN, NP, PQ, QM. Ngũ giác ABCDE ở Hình 4b gồm 5 đỉnh A, B, C, D, E và 5 cạnh AB, BC, CD, DE, EA.
Quan sát hai hình đó, hãy cho biết các phát biểu sau là đúng hay sai:
Quảng cáo
Trả lời:
Giải bởi Vietjack
– Hình 4a:
⦁ đỉnh M là điểm chung của 2 cạnh MN, MQ;
⦁ đỉnh N là điểm chung của 2 cạnh NM, NP;
⦁ đỉnh P là điểm chung của 2 cạnh PN, PQ;
⦁ đỉnh Q là điểm chung của 2 cạnh QM, QP.
– Hình 4b:
⦁ đỉnh A là điểm chung của 2 cạnh AB, AE;
⦁ đỉnh B là điểm chung của 2 cạnh BA, BC;
⦁ đỉnh C là điểm chung của 2 cạnh CB, CD;
⦁ đỉnh D là điểm chung của 2 cạnh DC, DE;
⦁ đỉnh E là điểm chung của 2 cạnh EA, ED.
Vậy phát biểu a) là đúng.
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
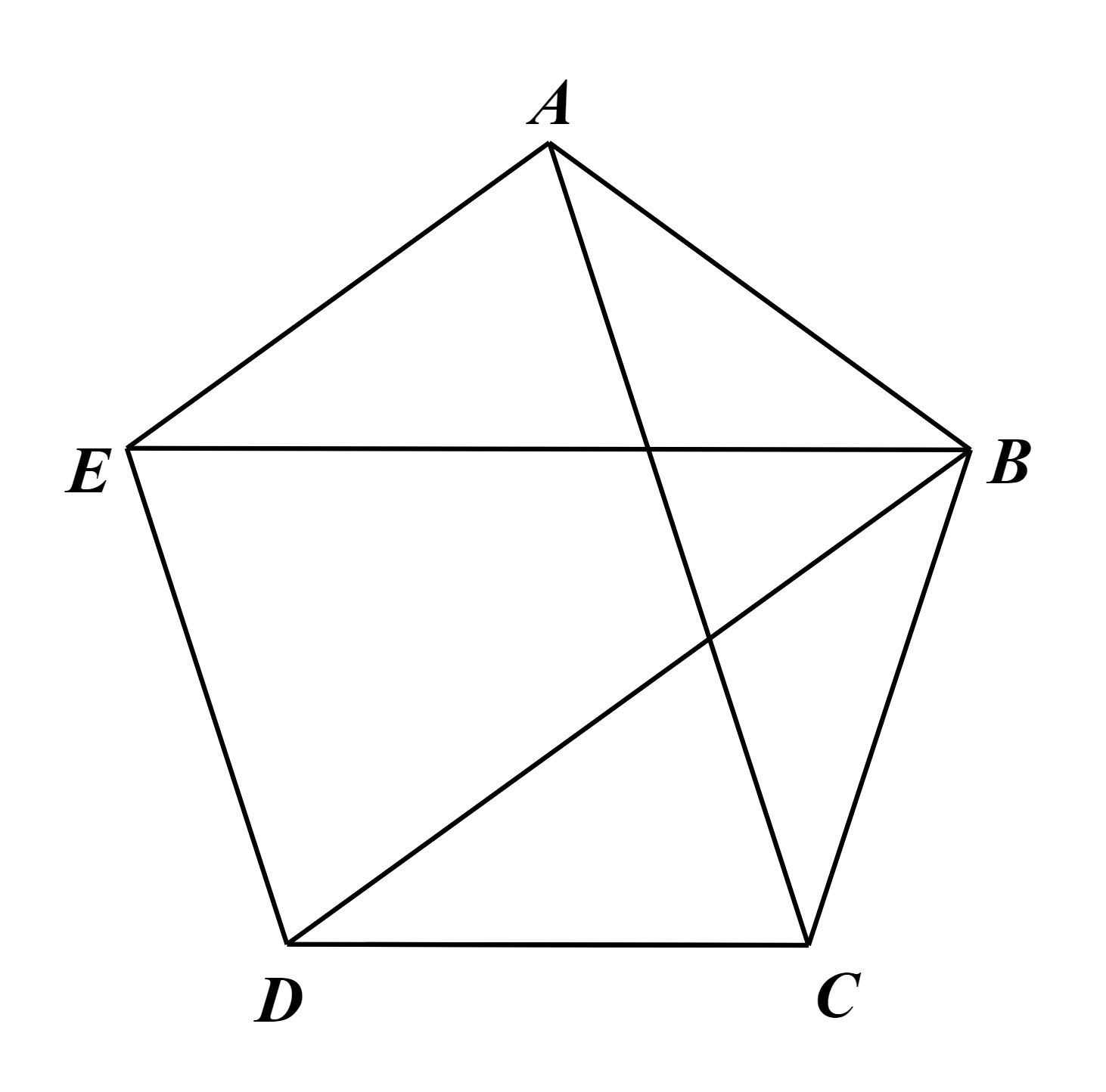
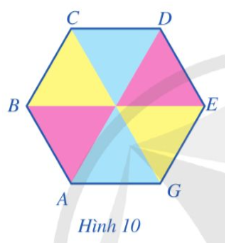
⦁ Do ngũ giác ABCDE có các cạnh bằng nhau nên AB = BC = CD = DE = EA.
Xét ∆ABE có AB = AE nên ∆ABE cân tại A, suy ra 
Lại có 
(tổng ba góc của một tam giác)
Suy ra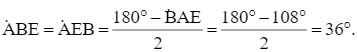 
Chứng minh tương tự với ∆BCD ta cũng có 
Ta có: 
Suy ra 
⦁ Xét ∆ABE và ∆CDB có:
AB = CD; 
AE = CB
Do đó ∆ABE = ∆CDB (c.g.c)
Suy ra BE = BD (hai cạnh tương ứng)
Nên ∆BDE cân tại B, suy ra 
Lại có 
(tổng ba góc của một tam giác)
Suy ra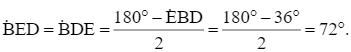 
Khi đó: 
Và 
Như vậy, 
Vậy ngũ giác ABCDE có 5 cạnh bằng nhau và 5 góc bằng nhau nên ABCDE là ngũ giác đều.
Lời giải
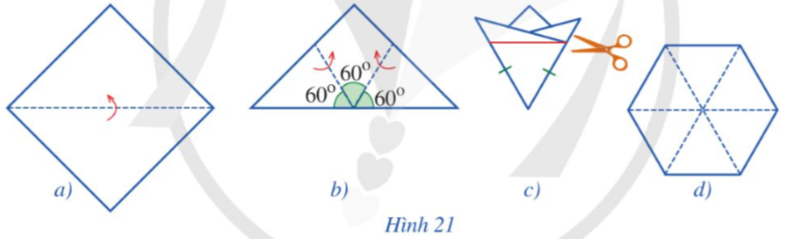
Theo cách bạn Đan làm thì khi mở ra sẽ được một hình lục giác tạo bởi 6 tam giác đều (tam giác cân có góc ở đỉnh là 60°) nên theo kết quả của Luyện tập, trang 83, SGK Toán lớp 9, Tập 2 thì hình được tạo ra chính là một lục giác đều.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập