Câu hỏi:
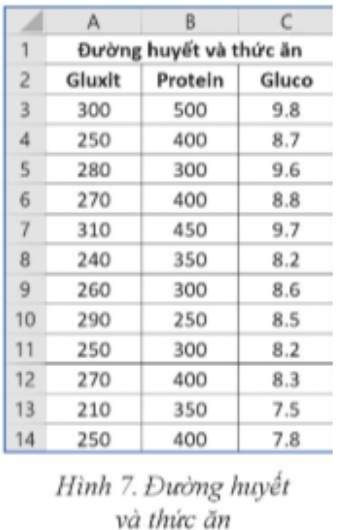
03/07/2024 51Hãy sử dụng Excel để thực hiện các công việc sau:
1) Nhập số gam tinh bột (Gluxit), chất đạm (Protein) và chỉ số đường huyết (Gluco) của một người như ở Hình 7.
2) Kiểm tra và cho biết từng dãy số liệu (Gluxit và Protein) có được xem là phân phối chuẩn không.
3) Nếu các dãy số liệu trên có phân phối chuẩn, hãy thực hiện phép kiểm định cần thiết để cho biết giá trị trung bình của hai dãy số liệu có khác biệt về mặt thống kê hay không.
4) Kiểm tra và cho biết giữa tinh bột và chất đạm, chất nào ảnh hưởng đến chỉ số đường huyết nhiều hơn.
Sách mới 2k7: 30 đề đánh giá năng lực DHQG Hà Nội, Tp. Hồ Chí Minh, BKHN 2025 mới nhất (600 trang - chỉ từ 160k).
Quảng cáo
Trả lời:
Các bước chi tiết khái quát cho từng bước sử dụng Excel để thực hiện các công việc:
1) Nhập dữ liệu: Mở một tệp Excel mới. Tạo các tiêu đề cho các cột dữ liệu: "Gluxit", "Protein", "Gluco". Nhập dữ liệu tương ứng vào các ô trong cột Gluxit, Protein và Gluco.
2) Kiểm tra xem giữa tinh bột và chất đạm, chất nào ảnh hưởng đến chỉ số đường huyết nhiều hơn.
Chọn một ô trống để hiển thị kết quả kiểm tra phân phối chuẩn.
Sử dụng hàm Excel =NORM.DIST() để kiểm tra xem dãy dữ liệu có phân phối chuẩn hay không.
Sử dụng công thức sau:
=NORM.DIST(A2, AVERAGE($A$2:SA$N), STDEV($A$2:SA$N), TRUE)
Trong đó:
A2 là giá trị cần kiểm tra. $A$2:SA$N là dãy dữ liệu trong cột Gluxit (tương tự cho cột Protein).
AVERAGE($A$2:SA$N) và STDEV($A$2:SA$N) lần lượt là giá trị trung bình và độ lệch chuẩn của dãy dữ liệu Gluxit (tương tự cho cột Protein).
Kéo công thức xuống dưới để áp dụng cho tất cả các giá trị trong cột Gluxit và Protein.
Nếu giá trị trả về gần với 0.5 (khoảng từ 0.4 đến 0.6), dãy dữ liệu có thể được coi là phân phối chuẩn.
3) Kiểm định giá trị trung bình
Sử dụng phép kiểm định t dựa trên hàm T.TEST() trong Excel.
Chọn một ô trống để hiển thị kết quả kiểm định giá trị trung bình.
Sử dụng công thức sau: =T.TEST(A2:A100, B2:B100, 2, 2)
Trong đó:
A2:A100 và B2:B100 là dãy dữ liệu Gluxit và Protein.
2 đại diện cho loại kiểm định (2-tailed).
2 đại diện cho loại phân phối (2-sample equal variance).
Giá trị trả về sẽ là p-value. Nếu p-value nhỏ hơn một ngưỡng nhất định (ví dụ: 0.05), ta có thể kết luận rằng giá trị trung bình của hai dãy số liệu có sự khác biệt đáng kể.
4) Phân tích ảnh hưởng
Sử dụng hàm CORREL() để tính toán hệ số tương quan giữa Gluxit, Protein và Gluco.
Sử dụng công thức sau:
=CORREL(A2:A100, C2:C100) Và =CORREL(B2:B100, C2:C100) để tính toán hệ số tương quan giữa Gluxit và Gluco, và giữa Protein và Gluco.
So sánh giá trị tương quan của Gluxit với Gluco và Protein với Gluco để xác định chất nào ảnh hưởng nhiều hơn đến chỉ số đường huyết.
Đã bán 152
Đã bán 114
Đã bán 132
Đã bán 47
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong các câu sau về kiểm định giả thuyết thống kê, những câu nào đúng?
a) Độ tin cậy của một phép kiểm định giả thuyết thống kê lên đến 99% nếu xác suất mắc sai lầm là 1%.
b) Trong kiểm định F, nếu F Critical one-tail < F < 1 thi bác bỏ giả thuyết H
c) Trong kiểm định t - Test, nếu t Stat nằm trong khoảng (-t Critical two-tail, t Critical two-tail) thì chấp nhận H.
d) Phân tích tương quan tuyến tính giúp kiểm tra dược hai biến ngẫu nhiên có mối quan hệ phụ thuộc lẫn nhau hay không.
Câu 2:
Bảng tính ở Hình 1 thể hiện hai dãy điểm thi sức bền của hai nhóm học sinh A và B sau cùng một thời gian rèn luyện theo hai phương pháp khác nhau: nhóm A theo phương pháp chạy bộ truyền thống, nhóm B theo phương pháp mới là bơi lội. Một người nói rằng: "Chênh lệch điểm trung bình giữa hai nhóm A và B là không đáng kể (7.696 - 7.173 = 0.523), nên có thể nói rằng phương pháp mới không làm thay đổi hiệu quả rèn luyện sức bền khi so với phương pháp truyền thống". Em có đồng ý với ý kiến này không và tại sao?
Câu 3:
Hãy sử dụng Excel tạo bảng tính như ở Hình 1 và thực hiện các yêu cầu sau:
1) Tính toán thống kê: Tính số trung bình và độ lệch chuẩn của hai mẫu A và B. Từ đó, hãy nhận xét về tính đại diện của các số trung bình.
2) Kiểm định giả thuyết thống kê: Hãy thực hiện phép kiểm định giả thuyết thống kê phù hợp để cho biết nhận xét của người nói trong Hoạt động khởi động có đúng về mặt thống kê hay không?
Câu 4:
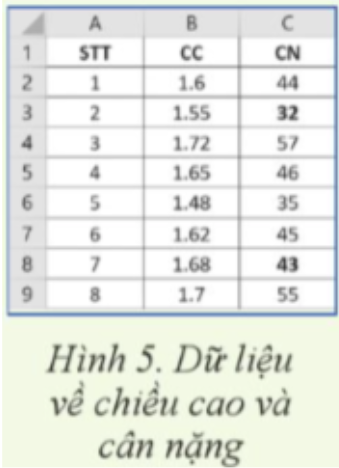
Bảng tính ở Hình 5 là dữ liệu vẻ chiếu cao (CC) và cần nặng (CN) của một nhóm người (một mẫu) được rút trích từ một cơ sở dữ liệu điều tra sức khỏe toàn dân (tổng thể) của Bộ Y tế. Em hãy sử dụng Excel nhập dữ liệu đã cho và phần tích dữ liệu để trả lời các câu hỏi sau: Liệu giữa chiều cao và cân nặng có mối tương quan với nhau không? Nếu có thì mức độ tương quan giữa chiều cao và cân nặng là bao nhiêu?
Gọi 084 283 45 85
Hỗ trợ đăng ký khóa học tại Vietjack
về câu hỏi!