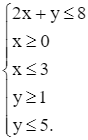Câu hỏi:

12/07/2024 375

Xét tình huống thương nhân thu mua trái cây ở Hoạt động khởi động (trang 6).
Từ đó, phát biểu bài toán quy hoạch tuyến tính tìm khối lượng thu mua mỗi loại trái cây để thu được lợi nhuận cao nhất. Giải bài toán đó.

Xem lời giải

Câu hỏi trong đề: Giải chuyên đề Toán 12 CTST Bài 1. Bài toán quy hoạch tuyến tính có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Lợi nhuận thương nhân thu được là F = 1,1x + 1,5y (triệu đồng).

Từ đó, ta nhận được bài toán quy hoạch tuyến tính:

F = 1,1x + 1,5y → max

với ràng buộc

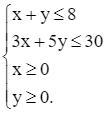
Giải bài toán trên như sau:

Viết lại ràng buộc của bài toán thành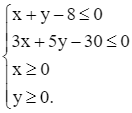

Tập phương án Ω của bài toán là miền tứ giác OABC như hình dưới đây với các đỉnh O(0; 0), A(8; 0), B(5; 3) và C(0; 6).

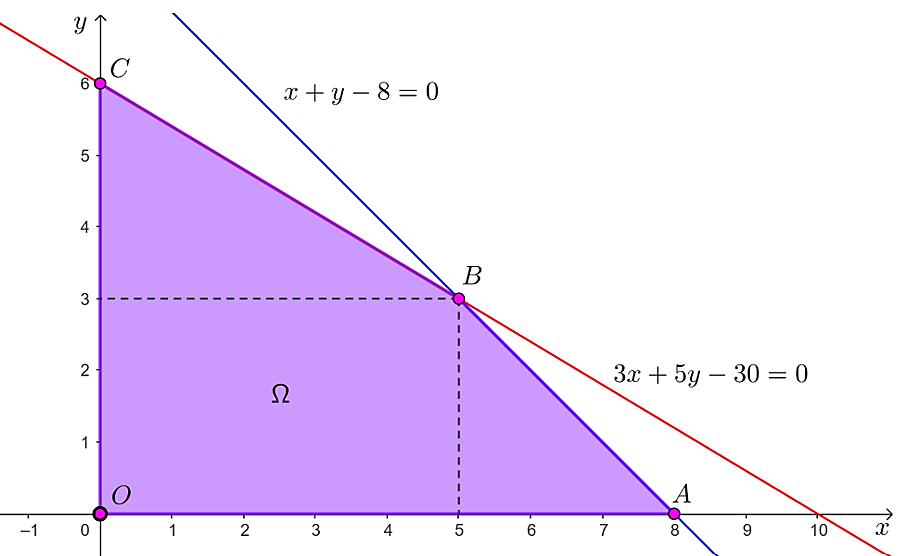
Giá trị của F tại các đỉnh:

F(0; 0) = 0;

F(8; 0) = 1,1 ∙ 8 + 1,5 ∙ 0 = 8,8;

F(5; 3) = 1,1 ∙ 5 + 1,5 ∙ 3 = 10;

F(0; 6) = 1,1 ∙ 0 + 1,5 ∙ 6 = 9.

Do đó, , đạt được khi x = 5, y = 3.

Vậy thương nhân nên mua 5 tấn trái cây loại A và 3 tấn trái cây loại B thì thu được lợi nhuận cao nhất là 10 triệu đồng khi bán hết hàng đã thu mua.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một cơ sở đóng thuyền thủ công cần 10 giờ lao động để đóng một thuyền loại A và 15 giờ lao động để đóng một thuyền loại B. Mỗi tuần cơ sở bổ trí được tối đa 120 giờ lao động cho việc đóng hai loại thuyền này. Qua thực tế, người ta thấy mỗi tuần cơ sở bán được tối đa 6 thuyền loại A và tối thiểu 2 thuyền loại B. Mỗi thuyền loại A, loại B cho lợi nhuận lần lượt là 0,5 triệu đồng và 0,7 triệu đồng. Mỗi tuần cơ sở nên đóng bao nhiêu thuyền mỗi loại để có thể thu được lợi nhuận cao nhất?

Xem đáp án

Lời giải

Gọi x, y (x ≥ 0, y ≥ 0) lần lượt là số chiếc thuyền loại A và B được đóng trong một tuần.

Khi đó, lợi nhuận thu được mỗi tuần là P = 0,5x + 0,7y (triệu đồng).

Vì mỗi tuần cơ sở bán được tối đa 6 thuyền loại A và tối thiểu 2 thuyền loại B nên ta có x ≤ 6 và y ≥ 2.

Do mỗi tuần cơ sở bổ trí được tối đa 120 giờ lao động cho việc đóng hai loại thuyền nên ta có 10x + 15y ≤ 120 hay 2x + 3y ≤ 24.

Từ đó, ta nhận được bài toán quy hoạch tuyến tính:

P = 0,5x + 0,7y → max

Với ràng buộc

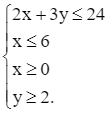
Tập phương án Ω của bài toán là miền tứ giác ABCD được tô màu như hình dưới đây với các đỉnh A(0; 2), B(6; 2), C(6; 4) và D(0; 8).

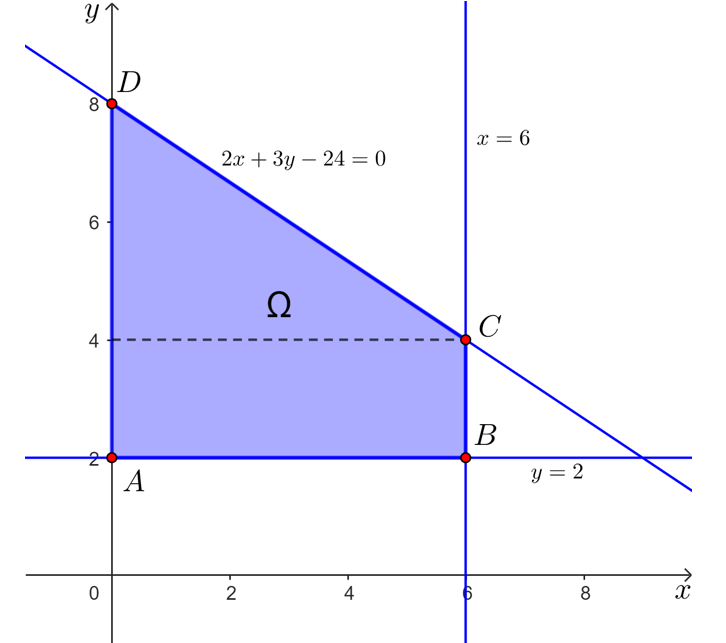
Giá trị của P tại các đỉnh:

P(0; 2) = 0,5 ∙ 0 + 0,7 ∙ 2 = 1,4;

P(6; 2) = 0,5 ∙ 6 + 0,7 ∙ 2 = 4,4;

P(6; 4) = 0,5 ∙ 6 + 0,7 ∙ 4 = 5,8;

P(0; 8) = 0,5 ∙ 0 + 0,7 ∙ 8 = 5,6.

Do đó, , đạt được khi x = 6, y = 4.

Vậy mỗi tuần cơ sở đó nên đóng 6 chiếc thuyền loại A và 4 chiếc thuyền loại B thì thu được lợi nhuận cao nhất là 5,8 triệu đồng.

Câu 2

Một dây chuyền của nhà máy sản xuất đá xây dựng dự định sản xuất hai loại sản phẩm A và B. Thời gian để dây chuyền sản xuất 100 tấn sản phẩm loại A và 100 tấn sản phẩm loại B lần lượt là 2 giờ và 3 giờ. Do nhu cầu thị trường, xí nghiệp sản xuất sản lượng sản phẩm loại A không ít hơn 3 lần sản lượng sản phẩm loại B. Sản phẩm loại A cho lợi nhuận là 5 triệu đồng/100 tấn; sản phẩm loại B cho lợi nhuận 9 triệu đồng/100 tấn. Trong thời gian không quá 6 giờ làm việc của dây chuyền, cần sản xuất bao nhiêu tấn sản phẩm loại A, bao nhiêu tấn sản phẩm loại B để thu được lợi nhuận cao nhất?

Xem đáp án

Lời giải

Gọi x, y (x ≥ 0, y ≥ 0, tính theo tấn) lần lượt là khối lượng sản phẩm loại A và sản phẩm loại B cần sản xuất. Khi đó lợi nhuận thu được là P = 0,05x + 0,09y (triệu đồng).

Vì xí nghiệp sản xuất sản lượng sản phẩm loại A không ít hơn 3 lần sản lượng sản phẩm loại B nên x ≥ 3y.

Do thời gian để làm việc của dây chuyền không quá 6 giờ nên 0,02x + 0,03y ≤ 6.

Từ đó, ta nhận được bài toán quy hoạch tuyến tính:

P = 0,05x + 0,09y → max

với ràng buộc

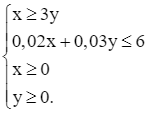
Tập phương án Ω của bài toán là miền tam giác OAB trên hình dưới đây với các đỉnh O(0; 0), A(300; 0) và .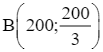

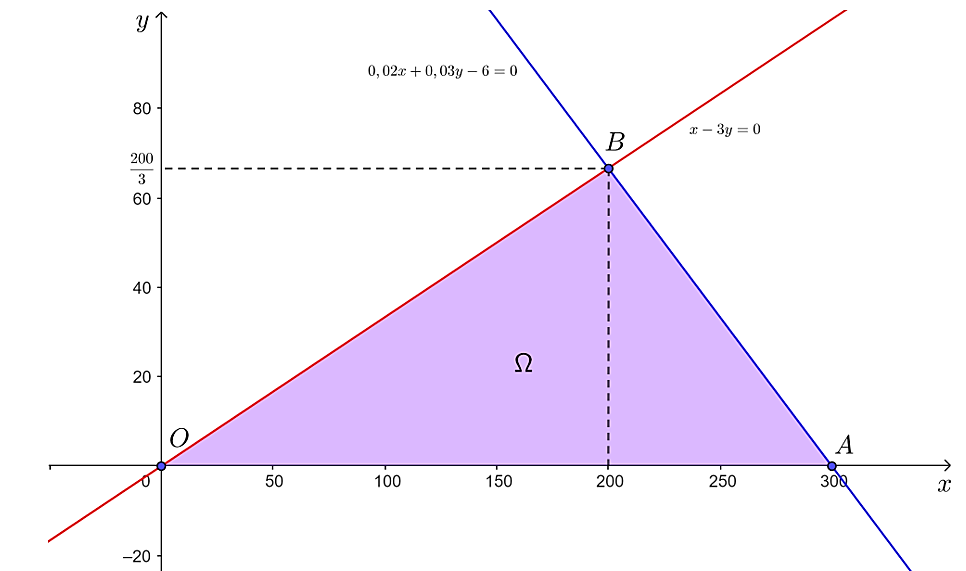
Giá trị của P tại các đỉnh:

P(0; 0) = 0;

P(300; 0) = 0,05 ∙ 300 + 0,09 ∙ 0 = 15;

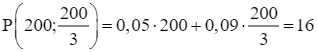Do đó, , đạt được khi x = 200, .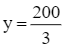

Vậy trong thời gian không quá 6 giờ làm việc của dây chuyền, cần sản xuất 200 tấn sản phẩm loại A và tấn sản phẩm loại B để thu được lợi nhuận cao nhất.