Bạn Dung tham gia trò chơi ném phi tiêu trúng thưởng với luật chơi như sau: Ở mỗi lượt chơi, bạn Dung ném một mũi phi tiêu. Nếu bạn Dung ném được vào vòng 10 điểm, bạn Dung được thưởng 2 quả bóng bay; nếu ném được vòng 9 điểm, bạn Dung được thưởng 1 quả bóng bay. Nếu không ném được vào vòng 9 hay 10 điểm thì bạn Dung không được thưởng. Gọi X là số bóng bay bạn Dung được thưởng trong một lượt chơi. Lập bảng phân bố xác suất của X biết rằng xác suất bạn Dung ném được vào vòng 10 điểm là 0,1 và vòng 9 điểm là 0,2.
Bạn Dung tham gia trò chơi ném phi tiêu trúng thưởng với luật chơi như sau: Ở mỗi lượt chơi, bạn Dung ném một mũi phi tiêu. Nếu bạn Dung ném được vào vòng 10 điểm, bạn Dung được thưởng 2 quả bóng bay; nếu ném được vòng 9 điểm, bạn Dung được thưởng 1 quả bóng bay. Nếu không ném được vào vòng 9 hay 10 điểm thì bạn Dung không được thưởng. Gọi X là số bóng bay bạn Dung được thưởng trong một lượt chơi. Lập bảng phân bố xác suất của X biết rằng xác suất bạn Dung ném được vào vòng 10 điểm là 0,1 và vòng 9 điểm là 0,2.
Quảng cáo
Trả lời:
Tập hợp các giá trị có thể của X là: {0; 1; 2}.
Xác suất bạn Dung không được thưởng bóng bay là:
P(X = 0) = 1 – P(X = 1) – P(X = 2) = 1 – 0,2 – 0,1 = 0,7.
Vậy ta có bảng phân bố xác suất cho biến ngẫu nhiên rời rạc X như sau:
|
X |
0 |
1 |
2 |
|
P |
0,7 |
0,2 |
0,1 |
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
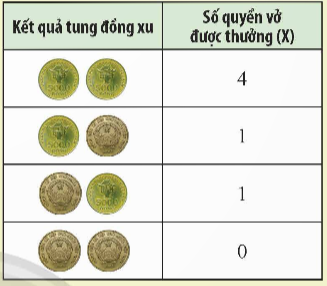
Gọi X là số tiền thu về cho một lần chơi.
Vì trong một lần chơi thì số tiền thu về có thể là:
⦁ –1 000 đồng nếu không có quả bóng nào cùng số với hộp;
⦁ 1 000 đồng nếu có đúng một quả bóng cùng số với hộp;
⦁ 5 000 đồng nếu cả ba quả bóng đều cùng số với hộp.
Vậy tập giá trị của X là: {–1 000; 1 000; 5 000}.
Tổng số kết quả có thể xảy ra khi đặt 3 quả bóng vào 3 cái hộp là: n(Ω) = 3! = 6.
– Biến cố “X bằng –1 000” xảy ra khi không có quả bóng nào cùng số với hộp. Số kết quả thuận lợi cho biến cố “X bằng –1 000” là: 2 . 1 . 1 = 2.
Xác suất của biến cố “X bằng –1 000” là: 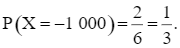
– Biến cố “X bằng 1 000” xảy ra khi có đúng một quả bóng cùng số với hộp. Số kết quả thuận lợi cho biến cố “X bằng 1 000” là: (1 . 1 . 1) . 3 = 3.
Xác suất của biến cố “X bằng 1 000” là: 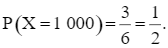
– Biến cố “X bằng 5 000” xảy ra khi cả ba quả bóng đều cùng số với hộp. Số kết quả thuận lợi cho biến cố “X bằng 5 000” là: 1.
Xác suất của biến cố “X bằng 5 000” là: 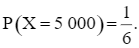
Ta có bảng phân bố xác suất của X là:
|
X |
–1 000 |
1 000 |
5 000 |
|
P |
|
|
|
Kì vọng của X là:
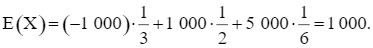
Ta thấy E(X) > 0 nên nếu so sánh về mặt trung bình thì người chơi có lợi hơn.
Lời giải
Y là biến cố ngẫu nhiên rời rạc và nhận các giá trị trong tập hợp {2; 3}.
Tổng số kết quả có thể xảy ra khi chọn ngẫu nhiên đồng thời 2 thẻ từ hộp là: n(Ω) = 3.
Do chỉ có một trường hợp xảy ra mà số lớn hơn trong hai số ghi trên hai thẻ đó là 2 (một thẻ ghi số 1 và một thẻ ghi số 2) nên số kết quả thuận lợi cho biến cố “Y bằng 2” là 1.
Xác suất của biến cố “Y = 2” là: 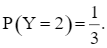
Tương tự, ta có 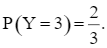
Bảng phân bố xác suất của Y là:
|
Y |
2 |
3 |
|
P |
|
|
Kì vọng của Y là:
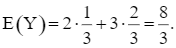
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.