Đọc văn bản sau và trả lời các câu hỏi từ 35 đến 41:
Staphylococcus aureus (S. Aureus) là một chủng vi khuẩn được tìm thấy trên da của người khỏe mạnh mà không gây ra bất kỳ ảnh hưởng nào. Tuy nhiên, chúng lại sinh trưởng mạnh mẽ và có khả năng gây bệnh và truyền bệnh thông qua thực phẩm, đặc biệt là ở thịt đã qua xử lý, hoặc được nấu chín. Cần phải xác định các điều kiện thúc đẩy sự phát triển của các loài vi khuẩn gây bệnh này và áp dụng kiến thức đó trong các giai đoạn sơ chế và xử lí thực phẩm. Hai nhóm sinh viên tiến hành các thí nghiệm nhằm xác định điều kiện sinh trưởng lý tưởng cho S. Aureus. Trong mỗi nhóm, vi khuẩn được cấy vào các môi trường dinh dưỡng khác nhau và phát triển trong một khoảng thời gian.
Máy đo quang phổ được sử dụng để phân tích sự phát triển của vi khuẩn trong môi trường chất lỏng, biết rằng độ đục càng tăng thì lượng vi khuẩn phát triển càng mạnh và giá trị đo được càng lớn.
Nhóm 1
Các sinh viên thực hiện thí nghiệm nhằm xác định nhiệt độ có ảnh hưởng đến tốc độ phát triển của S. Aureus trong môi trường giàu dinh dưỡng hay không. Họ cho chủng vi khuẩn phát triển trong môi trường giàu dinh dưỡng có độ pH là 6 ở các nhiệt độ sau: 3℃, 20℃, 37℃, 45℃ và 60℃. Các giá trị đo từ máy đo quang phổ được thể hiện ở bảng 1.
Bảng 1: Nuôi cấy chủng vi khuẩn ở các nhiệt độ và thời gian khác nhau
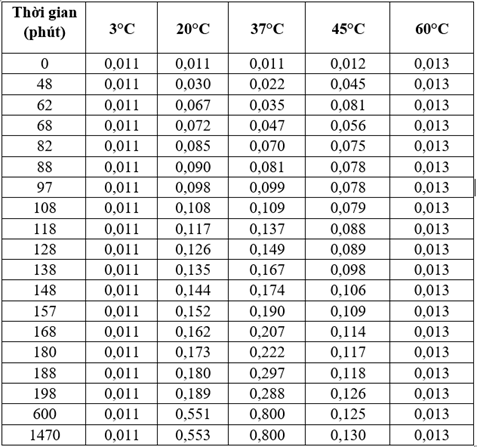
Nhóm 2
Các sinh viên thực hiện thí nghiệm nhằm xác định sự ảnh hưởng của pH đến sự phát triển của S. aureus. Họ cho chủng vi khuẩn phát triển trong môi trường giàu dinh dưỡng ở nhiệt độ 37℃ và độ pH lần lượt là 3, 5, 6, 7 và 9. Các giá trị đo từ máy đo quang phổ được thể hiện ở bảng 2.
Bảng 2: Nuôi cấy chủng vi khuẩn ở độ pH và thời gian khác nhau
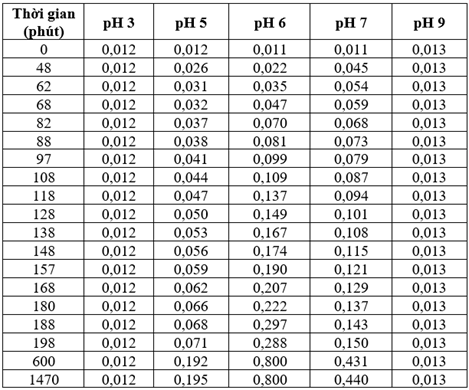
Phát biểu sau đây đúng hay sai?
Hai thí nghiệm trên, vi khuẩn đều được nuôi cấy trong môi trường nuôi cấy liên tục.
Đọc văn bản sau và trả lời các câu hỏi từ 35 đến 41:
Staphylococcus aureus (S. Aureus) là một chủng vi khuẩn được tìm thấy trên da của người khỏe mạnh mà không gây ra bất kỳ ảnh hưởng nào. Tuy nhiên, chúng lại sinh trưởng mạnh mẽ và có khả năng gây bệnh và truyền bệnh thông qua thực phẩm, đặc biệt là ở thịt đã qua xử lý, hoặc được nấu chín. Cần phải xác định các điều kiện thúc đẩy sự phát triển của các loài vi khuẩn gây bệnh này và áp dụng kiến thức đó trong các giai đoạn sơ chế và xử lí thực phẩm. Hai nhóm sinh viên tiến hành các thí nghiệm nhằm xác định điều kiện sinh trưởng lý tưởng cho S. Aureus. Trong mỗi nhóm, vi khuẩn được cấy vào các môi trường dinh dưỡng khác nhau và phát triển trong một khoảng thời gian.
Máy đo quang phổ được sử dụng để phân tích sự phát triển của vi khuẩn trong môi trường chất lỏng, biết rằng độ đục càng tăng thì lượng vi khuẩn phát triển càng mạnh và giá trị đo được càng lớn.
Nhóm 1
Các sinh viên thực hiện thí nghiệm nhằm xác định nhiệt độ có ảnh hưởng đến tốc độ phát triển của S. Aureus trong môi trường giàu dinh dưỡng hay không. Họ cho chủng vi khuẩn phát triển trong môi trường giàu dinh dưỡng có độ pH là 6 ở các nhiệt độ sau: 3℃, 20℃, 37℃, 45℃ và 60℃. Các giá trị đo từ máy đo quang phổ được thể hiện ở bảng 1.
Bảng 1: Nuôi cấy chủng vi khuẩn ở các nhiệt độ và thời gian khác nhau

Nhóm 2
Các sinh viên thực hiện thí nghiệm nhằm xác định sự ảnh hưởng của pH đến sự phát triển của S. aureus. Họ cho chủng vi khuẩn phát triển trong môi trường giàu dinh dưỡng ở nhiệt độ 37℃ và độ pH lần lượt là 3, 5, 6, 7 và 9. Các giá trị đo từ máy đo quang phổ được thể hiện ở bảng 2.
Bảng 2: Nuôi cấy chủng vi khuẩn ở độ pH và thời gian khác nhau

Phát biểu sau đây đúng hay sai?
Hai thí nghiệm trên, vi khuẩn đều được nuôi cấy trong môi trường nuôi cấy liên tục.
A. Đúng
B. Sai
Quảng cáo
Trả lời:
Sai. Vì môi trường nuôi cấy liên tục phải luôn được bổ sung chất dinh dưỡng, đồng thời lấy đi lượng dịch nuôi cấy tương đương. Mà trong hai thí nghiệm trên thì không có sự bổ sung dinh dưỡng, cũng không lấy ra lượng dịch nuôi cấy nào, quần thể vi khuẩn phát triển trên môi trường dinh dưỡng ban đầu, cho đến khi sử dụng hết chất dinh dưỡng – đây là dạng nuôi cấy không liên tục.
Chọn B
Câu hỏi cùng đoạn
Câu 2:
Dung dịch nuôi cấy vi khuẩn càng đục chứng tỏ
Theo đoạn thông tin: “..., biết rằng độ đục càng tăng thì lượng vi khuẩn phát triển càng mạnh và giá trị đo được càng lớn.”
Chọn C
Câu 3:
Nhóm vi khuẩn nào có cùng điều kiện thí nghiệm ở hai thí nghiệm trên?
Nhóm 1 thí nghiệm trong điều kiện: pH = 6 với các nhiệt độ khác nhau.
Nhóm 2 thí nghiệm trong điều kiện: nhiệt độ 37℃ với độ pH khác nhau.
→ Nhóm vi khuẩn được nuôi cấy trong cùng điều kiện là có độ pH = 6 và nhiệt độ 37℃.
Chọn B
Câu 4:
Điền từ/cụm từ vào chỗ trống sau đây:
Khi cạn kiệt chất dinh dưỡng, vi khuẩn sẽ bắt đầu pha (1) ________.
Điền từ/cụm từ vào chỗ trống sau đây:
Khi cạn kiệt chất dinh dưỡng, vi khuẩn sẽ bắt đầu pha (1) ________.
Đáp án
Khi cạn kiệt chất dinh dưỡng, vi khuẩn sẽ bắt đầu pha (1) suy vong.
Giải thích
Trong môi trường nuôi cấy không liên tục, quần thể vi khuẩn sẽ trải qua 4 pha: tiềm phát, lũy thừa, cân bằng, suy vong. Khi cạn kiệt chất dinh dưỡng, vi khuẩn sẽ bắt đầu pha suy vong, làm cho số lượng vi khuẩn giảm xuống nhanh chóng.
Câu 5:
Ở giá trị pH nào quần thể vi khuẩn S. Aureus KHÔNG có sự sinh trưởng?
Nhìn vào số liệu bảng 2, ta thấy tại môi trường dinh dưỡng có độ pH = 3 và pH = 9 thì không thấy sự thay đổi của giá trị độ đục ↔ không có sự sinh trưởng của quần thể vi khuẩn.
Chọn C
Câu 6:
Phát biểu nào sau đây là đúng khi nghiên cứu kết quả thí nghiệm của nhóm 1?
Nhìn vào số liệu bảng 1, ta thấy S. Aureus phát triển nhanh nhất để đạt độ đục cao nhất tại 37℃ (0,800) cao hơn nhiều so với các nhóm khác nên tại 37℃ chủng vi khuẩn này phát triển tối ưu.
Chọn B
Câu 7:
Phát biểu sau đây đúng hay sai?
Trong thí nghiệm của nhóm 1, ở nhiệt độ 37℃, pha cân bằng có thể bắt đầu sau 10 giờ kể từ khi nuôi cấy.
Phát biểu sau đây đúng hay sai?
Trong thí nghiệm của nhóm 1, ở nhiệt độ 37℃, pha cân bằng có thể bắt đầu sau 10 giờ kể từ khi nuôi cấy.
A. Đúng
B. Sai
Đúng. Nhìn vào số liệu bảng 1 ở nhiệt độ 37℃, ta thấy ở giai đoạn 600 phút (= 10 giờ) trở đi thì số lượng vi khuẩn có xu hướng chững lại, không tăng (duy trì ở mức cân bằng). Do lượng dinh dưỡng bắt đầu cạn kiệt, chất độc hại tích lũy nhiều, tỉ lệ vi khuẩn sinh ra cân bằng với tỉ lệ vi khuẩn chết đi.
Chọn A
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: “14”
Giải thích
Xét hàm số \(g\left( x \right) = f\left( {x - m} \right) - \frac{1}{2}{(x - m - 1)^2} + 2023\).
\(g'\left( x \right) = f'\left( {x - m} \right) - \left( {x - m - 1} \right)\). Xét phương trình \(g'\left( x \right) = 0{\rm{\;}}\) (1).
Đặt \(x - m = t\), phương trình (1) trở thành \(f'\left( t \right) - \left( {t - 1} \right) = 0 \Leftrightarrow f'\left( t \right) = t - 1{\rm{\;}}\) (2).
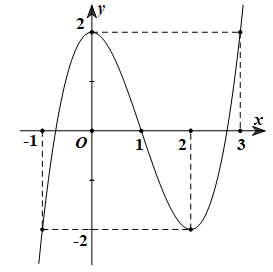
Nghiệm của phương trình \(\left( 2 \right)\) là hoành độ giao điểm của hai đồ thị \(y = f'\left( t \right)\) và \(y = t - 1\).
Ta có đồ thị các hàm số \(y = f'\left( t \right)\) và \(y = t - 1\) như sau:
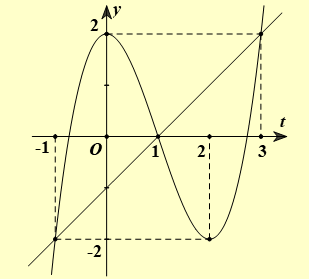
Căn cứ đồ thị các hàm số thì phương trình \(\left( 2 \right)\) có nghiệm là \(\left[ {\begin{array}{*{20}{c}}{t = - 1}\\{t = 1}\\{t = 3}\end{array} \Rightarrow \left[ {\begin{array}{*{20}{l}}{x = m - 1}\\{x = m + 1}\\{x = m + 3}\end{array}} \right.} \right.\)
Ta có bảng biến thiên của \(y = g\left( x \right)\) như sau:
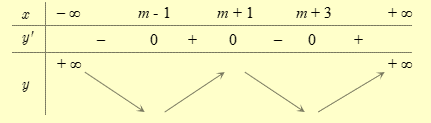
Để hàm số \(y = g\left( x \right)\) đồng biến trên khoảng \(\left( {5;6} \right)\) thì \(\left[ {\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{m - 1 \le 5}\\{m + 1 \ge 6}\end{array}} \right.}\\{m + 3 \le 5}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{5 \le m \le 6}\\{m \le 2}\end{array}} \right.\)
Vì \(m \in \mathbb{N}{\rm{*}} \Rightarrow m \in \left\{ {1;2;5;6} \right\} \Rightarrow S = 14\).
Lời giải
Đáp án
Một cửa hàng điện máy có doanh số bán lẻ tivi mỗi năm là 2500 chiếc. Chi phí lưu kho của mỗi chiếc tivi là 200 nghìn đồng một năm. Để đặt hàng nhà sản xuất, mỗi lần cửa hàng cần đặt cọc cố định là 10 triệu đồng và sau khi nhập hàng thì cần trả thêm 3 triệu đồng mỗi chiếc tivi. Biết rằng số lượng tivi trung bình gửi trong kho bằng một nửa số tivi của mỗi lần đặt hàng. Cửa hàng nên đặt hàng nhà sản xuất (1) ___5___ lần mỗi năm và mỗi lần đặt (2) __500__ chiếc tivi để chi phí hàng tồn kho là thấp nhất.
Giải thích
Gọi \(x\) là số tivi mỗi lần đặt hàng \(\left( {x \in \mathbb{N},x \in \left[ {1;2500} \right]} \right)\).
Khi đó, số lượng tivi trung bình gửi trong kho sẽ là \(\frac{x}{2}\). Do đó, chi phí gửi hàng trong kho mỗi năm sẽ là \(0,2.\frac{x}{2} = \frac{x}{{10}}\).
Số lần đặt hàng mỗi năm sẽ là \(\frac{{2500}}{x}\).
Do đó chi phí đặt hàng mỗi năm sẽ là \(\left( {10 + 3x} \right).\frac{{2500}}{x} = \frac{{25000}}{x} + 7500\).
Suy ra, chi phí hàng tồn kho là \(C\left( x \right) = \frac{x}{{10}} + \frac{{25000}}{x} + 7500\).
Bài toán trở thành tìm giá trị nhỏ nhất của \(C\left( x \right)\) với \(x \in \left[ {1;2500} \right]\).
Ta có: \(C'\left( x \right) = \frac{1}{{10}} - \frac{{25000}}{{{x^2}}},C'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 500}\\{x = - 500\left( L \right)}\end{array}} \right.\)
Bảng biến thiên:
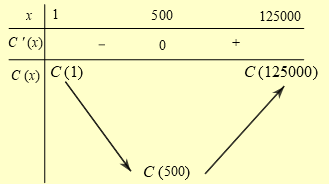
Vậy \(\mathop {{\rm{min}}}\limits_{\left[ {1;2500} \right]} C\left( x \right) = C\left( {500} \right) = 7600\)
Khi đó số lần đặt hàng mỗi năm sẽ là \(\frac{{2500}}{{500}} = 5\) lần.
Vậy để chi phí hàng tồn kho là nhỏ nhất thì cửa hàng cần đặt hàng 5 lần mỗi năm và 500 cái mỗi lần.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

![Diện tích mặt tròn xoay tạo thành khi quay đường cong \(f\left( x \right)\) quanh trục hoành giới hạn giữa hai mặt phẳng \(x = a,x = b\) được tính bởi công thức \(S = 2\pi \int\limits_a^b {\left| {f\left( x \right)} \right|\sqrt {1 + {{\left[ {f'\left( x \right)} \right]}^2}} {\rm{\;d}}x} \). Một bình hoa có dạng hình cầu khuyết như hình vẽ. Biết đường kính của bình hoa là \(20{\rm{\;cm}}\) và đường kính đáy/miệng của bình hoa là \(12{\rm{\;cm}}\). Diện tích tráng men mặt ngoài (kể cả đáy) của bình hoa bằng (1) _________ \(c{m^2}\). (Kết quả làm tròn đến chữ số thập phân thứ hai) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/11/blobid9-1731382856.png)