Câu hỏi:
12/07/2024 184
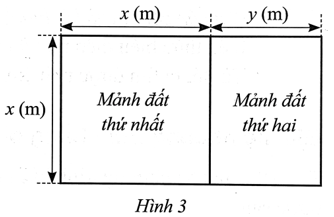
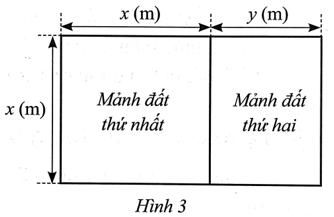
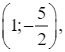Người ta chia một khu đất có dạng hình chữ nhật thành hai mảnh đất: mảnh đất thứ nhất có dạng hình vuông với độ dài cạnh x (m); mảnh đất thứ hai có dạng hình chữ nhật với chiều dài x (m) và chiều rộng y (m) (x > y > 0) được minh hoạ ở Hình 3. Chu vi của mảnh đất thứ nhất lớn hơn chu vi của mảnh đất thứ hai là 6,8 m. Trên một cạnh là chiều dài của khu đất, người ta đã xây một tường rào với chi phí 1 130 000 đồng theo giá 50 000 đồng/mét.
Cặp số (13; 9,6) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?
Người ta chia một khu đất có dạng hình chữ nhật thành hai mảnh đất: mảnh đất thứ nhất có dạng hình vuông với độ dài cạnh x (m); mảnh đất thứ hai có dạng hình chữ nhật với chiều dài x (m) và chiều rộng y (m) (x > y > 0) được minh hoạ ở Hình 3. Chu vi của mảnh đất thứ nhất lớn hơn chu vi của mảnh đất thứ hai là 6,8 m. Trên một cạnh là chiều dài của khu đất, người ta đã xây một tường rào với chi phí 1 130 000 đồng theo giá 50 000 đồng/mét.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xét cặp số (13; 9,6), thay x = 13; y = 9,6 vào mỗi phương trình trong hệ ta có:
13 ‒ 9,6 = 3,4;
13 + 9,6 = 22,6.
Suy ra cặp số (13; 9,6) là nghiệm của từng phương trình trong hệ.
Vậy cặp số (13; 9,6) có phải là nghiệm của hệ phương trình ở câu a.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Số tiền ba bạn dùng để mua bút bi là: 3 600x (đồng).
Số tiền ba bạn dùng để mua bút chì màu là: 5 000y (đồng).
Tổng số tiền ba bạn dùng để mua bút bi và bút chì màu là: 3 600x + 5 000y (đồng).
Số tiền ba bạn đã mua 3 quyển truyện là:
3 . 45 000 = 135 000 (đồng).
Số tiền còn lại dùng để mua bút bi xanh và bút chì màu là:
279 000 ‒ 135 000 = 144 000 (đồng).
Phương trình bậc nhất hai ẩn cho số tiền mà ba bạn đã dùng để mua bút bi, bút chì màu là:
3 600x + 5 000y = 144 000 hay 18x + 25y = 720.
Từ phương trình 18x + 25y = 720, ta suy ra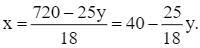 
Chọn y = 18, ta có x = 40 – 25 = 15.
Lời giải
⦁ Phương trình bậc nhất hai ẩn x, y có vô số nghiệm (x; y), mỗi nghiệm được biểu diễn bởi một điểm nằm trên đường thẳng 
Do đó phát biểu a) là sai.
⦁ Thay x = 4; y = 1 vào phương trình (1) ta có:
2.4 ‒ 3.1 = 5.
Suy ra, cặp số (4; 1) là một nghiệm của phương trình (1). Do đó phát biểu b) là đúng.
⦁ Thay x = ‒2; y = ‒3 vào phương trình (1) ta có:
2.(‒2) ‒ 3.(‒3) = 5.
Suy ra, cặp số (‒2; ‒3) là một nghiệm của phương trình (1). Do đó phát biểu c) là sai.
Vậy phát biểu b) là đúng, phát biểu a), c) là sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
-
Chuyên đề 8: Hình học (có đáp án)