Bác Lan có 500 triệu đồng để đầu tư vào hai khoản: trái phiếu và gửi tiết kiệm ngân hàng với kì hạn 12 tháng. Lãi suất của trái phiếu và gửi tiết kiệm ngân hàng lần lượt là 7%/năm và 6%/năm. Tính số tiền mà bác Lan đầu tư vào mỗi khoản để mỗi năm nhận được tiền lãi là 32 triệu đồng từ hai khoản đầu tư đó.
Bác Lan có 500 triệu đồng để đầu tư vào hai khoản: trái phiếu và gửi tiết kiệm ngân hàng với kì hạn 12 tháng. Lãi suất của trái phiếu và gửi tiết kiệm ngân hàng lần lượt là 7%/năm và 6%/năm. Tính số tiền mà bác Lan đầu tư vào mỗi khoản để mỗi năm nhận được tiền lãi là 32 triệu đồng từ hai khoản đầu tư đó.
Quảng cáo
Trả lời:
Gọi x (triệu đồng), y (triệu đồng) lần lượt là số tiền mà bác Lan đầu tư vào trái phiếu và gửi tiết kiệm ngân hàng với x > 0, y > 0.
Theo bài, tổng số tiền bác Lan đầu tư hai khoản là 500 triệu đồng nên ta có phương trình:
x + y = 500. (1)
Do lãi suất của trái phiếu là 7%/năm nên số tiền lãi bác Lan nhận được khi đầu tư trái phiếu là: x.7% = 0,07x (triệu đồng).
Do lãi suất của gửi tiết kiệm ngân hàng là 6%/năm nên số tiền lãi bác Lan nhận được khi gửi tiết kiệm ngân hàng là: y.6% = 0,06y (triệu đồng).
Theo bài, mỗi năm bác Lan nhận được tiền lãi là 32 triệu đồng từ hai khoản đầu tư đó nên ta có phương trình:
0,07x + 0,06y = 32. (2)
Từ (1) và (2) ta có hệ phương trình: 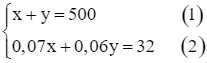
Từ phương trình (1), ta có x = 500 ‒ y. (3)
Thế vào phương trình (2) ta được: 0,07.(500 ‒ y) + 0,06y = 32. (4)
Giải phương trình (4):
0,07.(500 ‒ y) + 0,06y = 32
35 ‒ 0,07y + 0,06y = 32
‒0,01y = ‒3
y = 300.
Thay y = 300 vào phương trình (3) ta có:
x = 500 ‒ 300 = 200.
Ta thấy x = 200 và y = 300 thỏa mãn điều kiện nên hệ phương trình đã cho có nghiệm duy nhất (x; y) = (200; 300).
Vậy số tiền mà bác Lan đầu tư vào trái phiếu và gửi tiết kiệm ngân hàng lần lượt là 200 triệu đồng và 300 triệu đồng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Theo định luật bảo toàn nguyên tố đối với Fe và O, ta có:
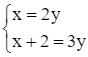 hay
hay 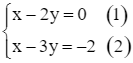
Trừ từng vế của hai phương trình (1) và (2), ta có: y = 2.
Thay y = 2 vào phương trình x = 2y ta có: x = 2.2 = 4.
Do đó, phương trình đã cho có nghiệm duy nhất (x; y) = (4; 2).
Vậy ta có phương trình sau cân bằng: 4FeO + O2 → 2Fe2O3.
Lời giải
Đổi 90 phút = 1,5 giờ; 30 phút = 0,5 giờ.
Gọi x (km) là quãng đường AB và y (giờ) là thời gian ô tô dự định đi với x > 0, y > 0,5.
Thời gian xe chạy quãng đường AB với tốc độ 40 km/h là: ![]() (giờ).
(giờ).
Thời gian xe chạy quãng đường AB với tốc độ 60 km/h là: ![]() (giờ).
(giờ).
Theo bài:
⦁ ô tô đi với tốc độ 40 km/h thì ô tô đến địa điểm B chậm hơn 90 phút so với dự định nên ta có phương trình:
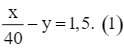
⦁ ô tô đi với tốc độ 60 km/h thì ô tô đến địa điểm B nhanh hơn 30 phút so với dự định nên ta có phương trình:
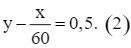
Từ (1) và (2) ta có hệ phương trình: 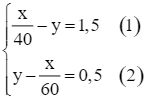
Cộng từng vế hai phương trình (1) và (2), ta nhận được phương trình:
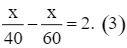
Giải phương trình (3):
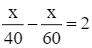
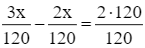
3x – 2x = 2.120
x = 240.
Thay x = 240 vào phương trình (1) ta có: 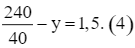
Giải phương trình (4):
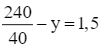
6 – y = 1,5
–y = –4,5
y = 4,5.
Ta thấy x = 240 và y = 4,5 thỏa mãn điều kiện nên hệ phương trình có nghiệm duy nhất (x; y) = (240; 4,5).
Vậy quãng đường AB dài 240 km và thời gian ô tô dự định đi là 4,5 giờ.
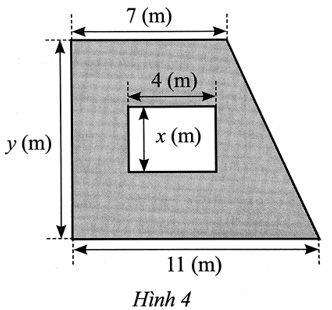
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.