Câu hỏi:
22/07/2024 7,102
Người ta làm mô hình kim tự tháp ở cổng vào của bảo tàng Louvre. Mô hình có dạng hình chóp tứ giác đều, chiều cao 21 m, độ dài cạnh đáy là 34 m.
a) Tính thể tích hình chóp.
b) Tính tổng diện tích các tấm kính để phủ kín bốn mặt bên hình chóp này, biết rằng người ta đo được độ dài cạnh bên của hình chóp là 31,92 m.
Người ta làm mô hình kim tự tháp ở cổng vào của bảo tàng Louvre. Mô hình có dạng hình chóp tứ giác đều, chiều cao 21 m, độ dài cạnh đáy là 34 m.
a) Tính thể tích hình chóp.
b) Tính tổng diện tích các tấm kính để phủ kín bốn mặt bên hình chóp này, biết rằng người ta đo được độ dài cạnh bên của hình chóp là 31,92 m.
Câu hỏi trong đề: Giải vở thực hành Toán 8 KNTT Luyện tập chung trang 121 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
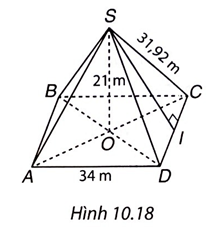
Hình 10.18 minh họa cho bài toán như sau.
a) Thể tích hình chóp tứ giác đều là:
\(V = \frac{1}{3}{S_{day}}.h = \frac{1}{3}{.34^2}.21 = 8092\) (m3).
Vậy thể tích hình chóp tứ giác đều là 8092 m3.
b) CI = 17m.
Áp dụng định lí Pythagore cho tam giác SCI vuông tại I, ta có:
CI2 + SI2 = SC2
172 + SI2 = 31,922
SI2 = 729,89
SI = 27,02
Diện tích xung quanh của hình chóp tứ giác đều là:
\[{S_{xp}} = p.d \approx \frac{{34.4}}{2}.27,02 = 1837,36\] (m2).
Vậy diện tích xung quanh hình chóp tứ giác đều là 1837,36 m2.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Theo đề bài ta có hình vẽ sau:
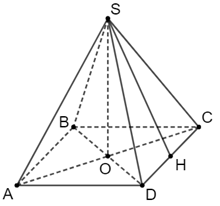
Diện tích xung quanh của đèn lồng là:
\({S_{xq}} = p.d = \frac{{40.4}}{2}.30 = 2400\) (cm2).
Vậy diện tích xung quanh của đèn lồng là 2400 cm2.
Lời giải
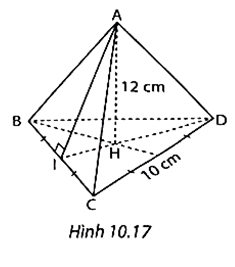
CI = 5. Áp dụng định lí Pythagore cho tam giác CDI vuông tại I, ta có:
CI2 + ID2 = CD2
52 + ID2 = 102
ID2 = 102 – 52 = 75
\(ID = \sqrt {75} \)
Diện tích đáy của hình chóp là \({S_{day}} = \frac{1}{2}ID.BC = \frac{1}{2}.8,66.10 = 43,3\) (cm2).
Thể tích hình chóp A.BCD là \(V = \frac{1}{3}{S_{day}}.h = \frac{1}{3}.43,3.12 = 173,2\) (cm3).
Vậy thể tích hình chóp A.BCD là 173,2 cm3.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 25
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Đề cuối kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án- Đề 2
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận