Giải vở thực hành Toán 8 KNTT Luyện tập chung trang 121
43 người thi tuần này 4.6 493 lượt thi 5 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Trắc nghiệm Các trường hợp đồng dạng của hai tam giác vuông lớp 8 (có đáp án)
Trắc nghiệm Định lí Pythagore và ứng dụng lớp 8 (có đáp án)
Trắc nghiệm Ba trường hợp đồng dạng của hai tam giác lớp 8 (có đáp án)
Trắc nghiệm Hai tam giác đồng dạng lớp 8 (có đáp án)
Đề kiểm tra Toán 8 Chương 5 (có đáp án) - Đề 2
Đề kiểm tra Toán 8 Chương 5 (có đáp án) - Đề 1
Bài tập ôn tập Toán 8 Chương 5 (có đáp án)
Trắc nghiệm Phép nhân và phép chia phân thức đại số lớp 8 (có đáp án)
Danh sách câu hỏi:
Lời giải
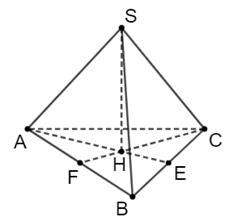
Thể tích của hình chóp tam giác đều S.ABC là:
\(V = \frac{1}{3}S.h = \frac{1}{3}.15,6.10 = 52\) (cm3).
Vậy thể tích của hình chóp tam giác đều S.ABC là 52 cm3.
Lời giải
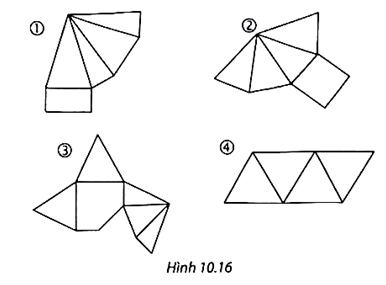
Hình 2 gấp và dán lại thành hình chóp tứ giác đều;
Hình 4 gấp và dán lại thành hình chóp tam giác đều.
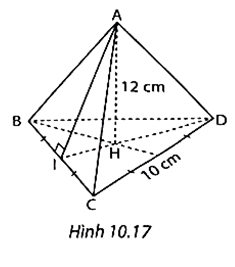
Lời giải
CI = 5. Áp dụng định lí Pythagore cho tam giác CDI vuông tại I, ta có:
CI2 + ID2 = CD2
52 + ID2 = 102
ID2 = 102 – 52 = 75
\(ID = \sqrt {75} \)
Diện tích đáy của hình chóp là \({S_{day}} = \frac{1}{2}ID.BC = \frac{1}{2}.8,66.10 = 43,3\) (cm2).
Thể tích hình chóp A.BCD là \(V = \frac{1}{3}{S_{day}}.h = \frac{1}{3}.43,3.12 = 173,2\) (cm3).
Vậy thể tích hình chóp A.BCD là 173,2 cm3.
Lời giải
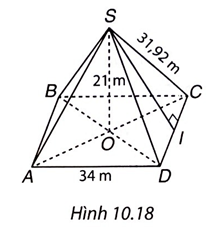
Hình 10.18 minh họa cho bài toán như sau.
a) Thể tích hình chóp tứ giác đều là:
\(V = \frac{1}{3}{S_{day}}.h = \frac{1}{3}{.34^2}.21 = 8092\) (m3).
Vậy thể tích hình chóp tứ giác đều là 8092 m3.
b) CI = 17m.
Áp dụng định lí Pythagore cho tam giác SCI vuông tại I, ta có:
CI2 + SI2 = SC2
172 + SI2 = 31,922
SI2 = 729,89
SI = 27,02
Diện tích xung quanh của hình chóp tứ giác đều là:
\[{S_{xp}} = p.d \approx \frac{{34.4}}{2}.27,02 = 1837,36\] (m2).
Vậy diện tích xung quanh hình chóp tứ giác đều là 1837,36 m2.
Lời giải
Theo đề bài ta có hình vẽ sau:
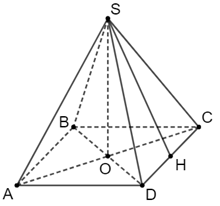
Diện tích xung quanh của đèn lồng là:
\({S_{xq}} = p.d = \frac{{40.4}}{2}.30 = 2400\) (cm2).
Vậy diện tích xung quanh của đèn lồng là 2400 cm2.
Nhắn tin Zalo
Hỏi bài tập