Giải VTH Toán 8 KNTT Luyện tập chung trang 108 có đáp án

39 người thi tuần này 4.6 450 lượt thi 5 câu hỏi

Đề số 1

🔥 Học sinh cũng đã học

59 người thi tuần này

Bài tập Bài toán thực tiễn liên quan đến thể tích, diện tích xung quanh của hình chóp tứ giác đều lớp 8 (có lời giải)

1 K lượt thi 10 câu hỏi

38 người thi tuần này

Bài tập Tính diện tích xung quanh và thể tích của hình chóp tứ giác đều lớp 8 (có lời giải)

1 K lượt thi 10 câu hỏi

37 người thi tuần này

Bài tập Bài toán thực tiễn liên quan đến tính thể tích, diện tích xung quanh của hình chóp tam giác đều lớp 8 (có lời giải)

1 K lượt thi 10 câu hỏi

42 người thi tuần này

Bài tập Tính diện tích xung quanh và thể tích của hình chóp tam giác đều lớp 8 (có lời giải)

1 K lượt thi 10 câu hỏi

37 người thi tuần này

Bài tập Các bài toán thực tiễn gắn với việc vận dụng các tam giác vuông đồng dạng lớp 8 (có lời giải)

1.1 K lượt thi 10 câu hỏi

45 người thi tuần này

Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore lớp 8 (có lời giải)

1.2 K lượt thi 10 câu hỏi

37 người thi tuần này

Bài tập Chứng minh các tính chất hình học lớp 8 (có lời giải)

1.2 K lượt thi 10 câu hỏi

40 người thi tuần này

Bài tập Tính độ dài cạnh trong tam giác vuông bằng cách sử dụng định lí Pythagore lớp 8 (có lời giải)

1.2 K lượt thi 10 câu hỏi

Danh sách câu hỏi:

Câu 1/5

Cho tam giác ABC vuông tại A và có đường cao AH. Biết rằng BH = 16 cm, CH = 9 cm.

a) Tính độ dài đoạn thẳng AH.

b) Tính độ dài đoạn thằng AB và AC.

Xem đáp án

Lời giải

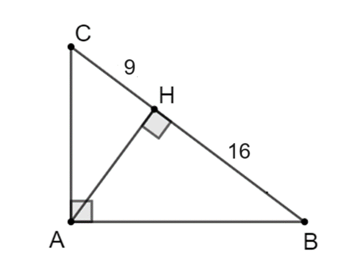
Cho tam giác ABC vuông tại A và có đường cao AH. Biết rằng BH = 16 cm, CH = 9 cm. (ảnh 1)

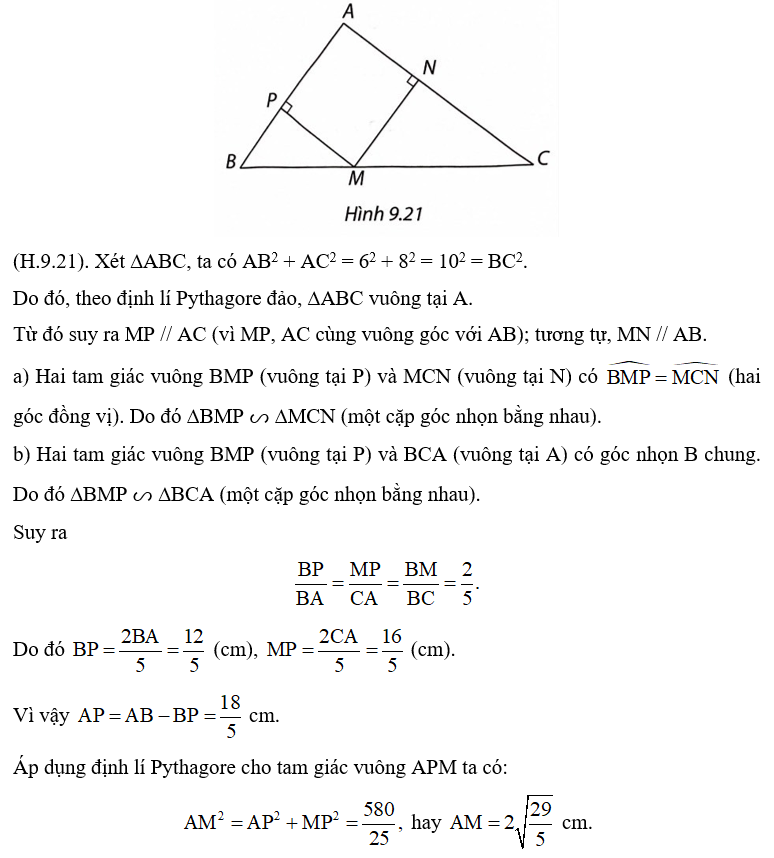
Áp dụng định lí Pythagore cho tam giác vuông AHB, ta có: AH² = AB² – BH².

Áp dụng định lí Pythagore cho tam giác buông AHC, ta có: AH² = AC² – CH².

Từ đó, ta có:

2AH² = (AB² – BH²) + (AC² – CH²) = BC² – BH² – CH² = 2.BH.CH.

Suy ra $A H = \sqrt{B H . C H} = 12$ (cm).

Áp dụng định lí Pythagore cho tam giác vuông AHB, ta có:

AB² = AH² + BH² = 400, hay AB = 20 (cm).

Áp dụng định lí Pythagore cho tam giác vuông AHC, ta có:

AC² = AH² + CH² = 225, hay AC = 15 (cm).

Câu 2/5

Cho tam giác ABC có AB = 6 cm, AC = 8 cm, BC = 10 cm. Cho điểm M nằm trên cạnh BC sao cho BM = 4 cm. Vẽ đường thẳng MN vuông góc với AC tại N và đường thẳng MP vuông góc với AB tại P.

a) Chứng minh ∆BMP ᔕ ∆MCN.

b) Tính độ dài đoạn thẳng AM.

Xem đáp án

Lời giải

Cho tam giác ABC có AB = 6 cm, AC = 8 cm, BC = 10 cm. Cho điểm M nằm (ảnh 1)

Câu 3/5

Trong Hình 9.22, cho AH, HE, HF lần lượt là các đường cao của các tam giác ABC, AHB, AHC. Chứng minh rằng:

a) ∆AEH ᔕ ∆AHB;

b) ∆AFH ᔕ ∆AHC;

c) ∆AFE ᔕ ∆ABC.

Xem đáp án

Lời giải

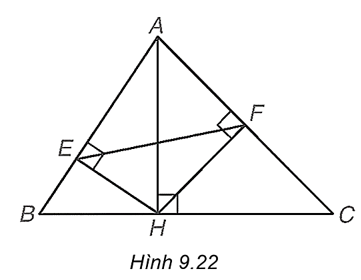
a) Hai tam giác vuông AEH (vuông tại E) và AHB (vuông tại H) có $\hat{E A H} = \hat{H A B}$ (góc chung).

Do đó ∆AEH ᔕ ∆AHB (g.g).

b) Hai tam giác vuông AFH (vuông tại F) và AHC (vuông tại H) có $\hat{F A H} = \hat{H A C}$ (góc chung).

Do đó ∆AFH ᔕ ∆AHC (g.g).

c) Vì ∆AEH ᔕ ∆AHB nên $\frac{A E}{A C} = \frac{A E}{A H} \cdot \frac{A H}{A C} = \frac{A H}{A B} \cdot \frac{A H}{A C} = \frac{A H^{2}}{A B \cdot A C} .$ (1)

Vì ∆AFH ᔕ ∆AHC nên $\frac{A F}{A B} = \frac{A F}{A H} \cdot \frac{A H}{A B} = \frac{A H}{A C} \cdot \frac{A H}{A B} = \frac{A H^{2}}{A B \cdot A C} .$ (2)

Từ (1) và (2) suy ra $\frac{A E}{A C} = \frac{A F}{A B} .$

Hai tam giác AFE và ABC có:

$\hat{A}$ chung; $\frac{A E}{A C} = \frac{A F}{A B}$ (theo chứng minh trên).

Do đó ∆AFE ᔕ ∆ABC (c.g.c).

Câu 4/5

Cho tam giác ABC vuông tại A có đường cao AH. Cho M và N lần lượt là trung điểm của AB và AC. Chứng minh ∆HBM ᔕ ∆HAN.

Xem đáp án

Lời giải

Cho tam giác ABC vuông tại A có đường cao AH. Cho M và N lần lượt (ảnh 1)

Câu 5/5

Vào gần buổi trưa, khi bóng bạn An dài 60 cm thì bóng cột cờ dài 3 m.

a) Biết rằng bạn An cao 1,4 m. Hỏi cột cờ cao bao nhiêu mét?

b) Vào buổi chiều khi bóng bạn An dài 3 m, hỏi bóng cột cờ dài bao nhiêu mét?

Xem đáp án

Lời giải

a) Do tam giác vuông có hai cạnh góc vuông là cột cờ và bóng cột cờ đồng dạng với tam giác vuông có hai cạnh góc vuông là An và bóng của An (vì góc tạo bởi cạnh huyền với mỗi chiếc bóng trong mỗi tam giác là góc tạo bởi tia nắng với chiếc bóng và chúng xem như bằng nhau do Mặt trời ở rất xa).

Vì vậy nếu gọi chiều cao cột cờ là h (m) thì ta có:

$\frac{h}{1, 4} = \frac{3}{0, 6},$ hay $h = \frac{3.1, 4}{0, 6} = 7$ (m).

b) Gọi chiều dài của bóng cột cờ là l (m) thì ta có:

$\frac{h}{1, 4} = \frac{l}{3},$ hay $l = \frac{3. h}{1, 4} = 15$ (m).

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Ôn vào 10

Ôn vào 6

ĐGNL-ĐGTD

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Toán

Toán

Toán

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Khoa học tự nhiên

Tin học

Lịch sử

Địa lí

Toán

Toán

Toán

Toán

Tiếng Việt

Tiếng Anh

Giải VTH Toán 8 KNTT Luyện tập chung trang 108 có đáp án

🔥 Học sinh cũng đã học

Bài tập Bài toán thực tiễn liên quan đến thể tích, diện tích xung quanh của hình chóp tứ giác đều lớp 8 (có lời giải)

Bài tập Tính diện tích xung quanh và thể tích của hình chóp tứ giác đều lớp 8 (có lời giải)

Bài tập Bài toán thực tiễn liên quan đến tính thể tích, diện tích xung quanh của hình chóp tam giác đều lớp 8 (có lời giải)

Bài tập Tính diện tích xung quanh và thể tích của hình chóp tam giác đều lớp 8 (có lời giải)

Bài tập Các bài toán thực tiễn gắn với việc vận dụng các tam giác vuông đồng dạng lớp 8 (có lời giải)

Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore lớp 8 (có lời giải)

Bài tập Chứng minh các tính chất hình học lớp 8 (có lời giải)

Bài tập Tính độ dài cạnh trong tam giác vuông bằng cách sử dụng định lí Pythagore lớp 8 (có lời giải)

Danh sách câu hỏi:

Cho tam giác ABC vuông tại A và có đường cao AH. Biết rằng BH = 16 cm, CH = 9 cm. a) Tính độ dài đoạn thẳng AH. b) Tính độ dài đoạn thằng AB và AC.

Cho tam giác ABC có AB = 6 cm, AC = 8 cm, BC = 10 cm. Cho điểm M nằm trên cạnh BC sao cho BM = 4 cm. Vẽ đường thẳng MN vuông góc với AC tại N và đường thẳng MP vuông góc với AB tại P. a) Chứng minh ∆BMP ᔕ ∆MCN. b) Tính độ dài đoạn thẳng AM.

Trong Hình 9.22, cho AH, HE, HF lần lượt là các đường cao của các tam giác ABC, AHB, AHC. Chứng minh rằng: a) ∆AEH ᔕ ∆AHB; b) ∆AFH ᔕ ∆AHC; c) ∆AFE ᔕ ∆ABC.

Cho tam giác ABC vuông tại A có đường cao AH. Cho M và N lần lượt là trung điểm của AB và AC. Chứng minh ∆HBM ᔕ ∆HAN.

Vào gần buổi trưa, khi bóng bạn An dài 60 cm thì bóng cột cờ dài 3 m. a) Biết rằng bạn An cao 1,4 m. Hỏi cột cờ cao bao nhiêu mét? b) Vào buổi chiều khi bóng bạn An dài 3 m, hỏi bóng cột cờ dài bao nhiêu mét?

Đăng ký

Đăng nhập

Quên mật khẩu

CHỌN BỘ SÁCH BẠN MUỐN XEM

Cho tam giác ABC vuông tại A và có đường cao AH. Biết rằng BH = 16 cm, CH = 9 cm.

a) Tính độ dài đoạn thẳng AH.

b) Tính độ dài đoạn thằng AB và AC.

Cho tam giác ABC có AB = 6 cm, AC = 8 cm, BC = 10 cm. Cho điểm M nằm trên cạnh BC sao cho BM = 4 cm. Vẽ đường thẳng MN vuông góc với AC tại N và đường thẳng MP vuông góc với AB tại P.

a) Chứng minh ∆BMP ᔕ ∆MCN.

b) Tính độ dài đoạn thẳng AM.

Trong Hình 9.22, cho AH, HE, HF lần lượt là các đường cao của các tam giác ABC, AHB, AHC. Chứng minh rằng:

a) ∆AEH ᔕ ∆AHB;

b) ∆AFH ᔕ ∆AHC;

c) ∆AFE ᔕ ∆ABC.

Vào gần buổi trưa, khi bóng bạn An dài 60 cm thì bóng cột cờ dài 3 m.

a) Biết rằng bạn An cao 1,4 m. Hỏi cột cờ cao bao nhiêu mét?

b) Vào buổi chiều khi bóng bạn An dài 3 m, hỏi bóng cột cờ dài bao nhiêu mét?