Giải SGK Toán 8 KNTT Bài 16. Đường trung bình của tam giác có đáp án

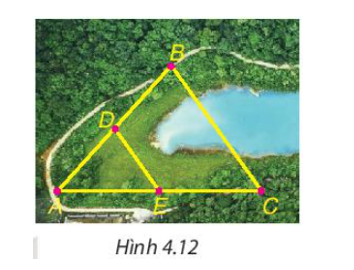
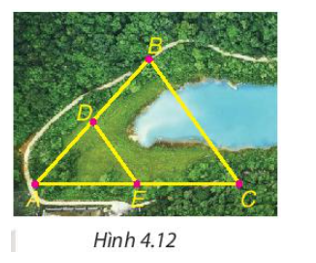
Sau bài học này ta giải quyết được bài toán như sau:

Trong tam giác ABC có D, E lần lượt là trung điểm của AB và AC nên D ∈ AB; E ∈ AC và AD = BD; AE = EC.

Suy ra DE là đường trung bình của tam giác ABC.

Do đó $DE=\frac{1}{2}BC$ suy ra BC = 2DE = 2 . 500 = 1 000 (m)

Vậy khoảng cách giữa hai điểm B và C bằng 1 000 m.

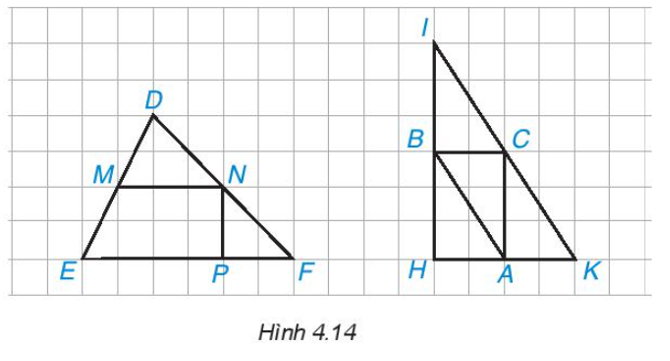
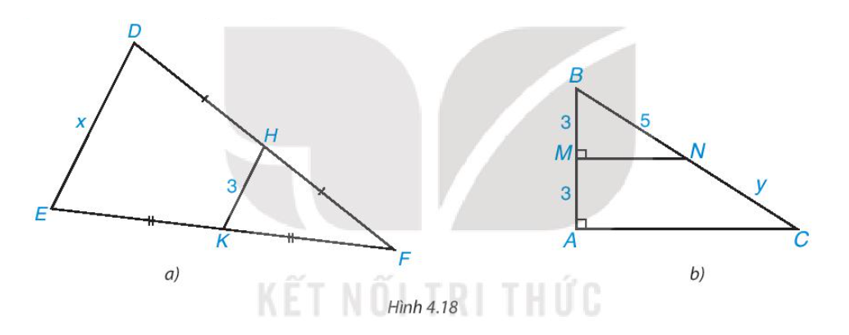
Quan sát Hình 4.14, ta thấy:

* Xét ∆DEF có M là trung điểm của cạnh DE; N là trung điểm của cạnh DF nên MN là đường trung bình của ∆DEF.

* Xét ∆IHK có:

• B là trung điểm của cạnh IH; C là trung điểm của cạnh IK nên BC là đường trung bình của ∆DEF.

• B là trung điểm của cạnh IH; A là trung điểm của cạnh HK nên AB là đường trung bình của ∆DEF.

• A là trung điểm của cạnh HK; C là trung điểm của cạnh IK nên AC là đường trung bình của ∆DEF.

Vậy đường trung bình của ∆DEF là MN; các đường trung bình của ∆IHK là AB, BC, AC.

Ta có AD = BD và D ∈ AB nên D là trung điểm của AB;

AE = EC và E ∈ AC nên E là trung điểm của AC.

Xét tam giác ABC có D, E lần lượt là trung điểm của AB và AC, theo định lí Thalès đảo, ta suy ra DE // BC (đpcm).

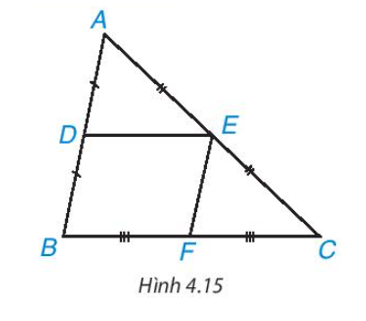
Vì DE là đường trung bình của tam giác ABC nên D, E lần lượt là trung điểm của AB, AC.

Suy ra $AD=\frac{1}{2}AB;AE=\frac{1}{2}AC$.

Do đó DE // BC (theo định lí Thalès đảo).

Vì E, F lần lượt là trung điểm của AC, BC.

Suy ra $EC=\frac{1}{2}AC;CF=\frac{1}{2}BC$.

Do đó EF // AB (theo định lí Thalès đảo).

Xét tứ giác DEFB có DE // BF (vì DE // BC); EF // BD (vì EF // AB)

Do đó tứ giác DEFB là hình bình hành.

Suy ra DE = BF mà $BF=\frac{1}{2}BC$ nên $DE=\frac{1}{2}BC$.

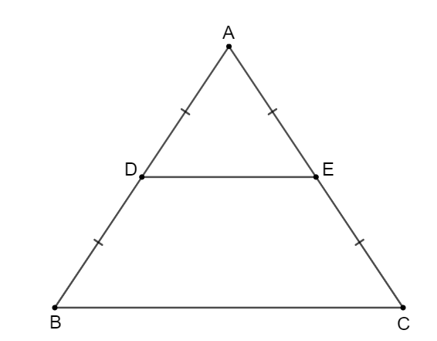
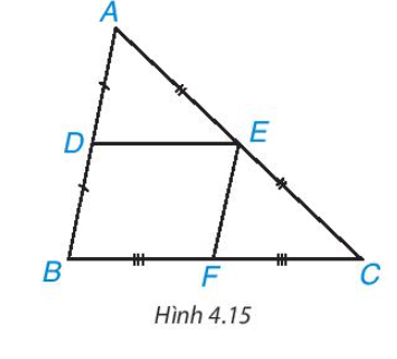
Tam giác ABC cân tại A nên $\widehat{B}=\widehat{C}$.

Vì D và E lần lượt là trung điểm của AB, AC nên DE là đường trung bình của tam giác ABC.

Suy ra DE // BC nên tứ giác DECB là hình thang.

Hình thang DECB có $\widehat{B}=\widehat{C}$ nên tứ giác DECB là hình thang cân.