Giải SBT Toán 8 KNTT Bài 11: Hình thang cân có đáp án

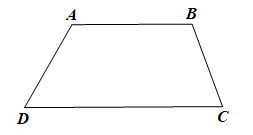
Trong hình thang ABCD có:

 $\widehat{A}$ và  $\widehat{D}$ là 2 góc bù nhau,  $\widehat{B}$ và  $\widehat{C}$ là 2 góc bù nhau.

Do đó  $\widehat{A}+\widehat{D}=180°$,  $\widehat{B}+\widehat{C}=180°$

Mà  $\widehat{A}=2\widehat{D}$ nên  $2\widehat{D}+\widehat{D}=180°$, suy ra  $\widehat{D}=60°$. Do đó  $\widehat{A}=2\widehat{D}=2\cdot 60°=120°.$

        $\widehat{B}=\widehat{C}+40°$ nên $\widehat{C}+40°+\widehat{C}=180°$, hay  $2\widehat{C}=140°$, suy ra  $\widehat{C}=70°$

Do đó  $\widehat{B}=\widehat{C}+40°=70°+40°=110°$

Vậy hình thang ABCD có  $\widehat{A}=120°;\widehat{B}=110°;\widehat{C}=70°;\widehat{D}=60°.$

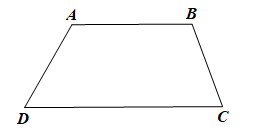
Xét hình thang ABCD có AB // CD

Ta có:

•  $\widehat{A}$ và  $\widehat{D}$ là hai góc kề với cạnh bên AD

Suy ra  $\widehat{A}+\widehat{D}=180°$ nên trong hai góc đó có có quá 1 góc tù

•  $\widehat{B}$ và  $\widehat{C}$ là hai góc kề với cạnh bên BC

Suy ra  $\widehat{B}+\widehat{C}=180°$ nên trong hai góc đó có có quá 1 góc tù

Do đó, trong bốn góc  $\widehat{A};\widehat{B;}\widehat{C};\widehat{D}$ có nhiều nhất 2 góc là góc tù.

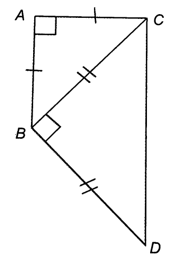
Do ∆ABC vuông cân tại đỉnh A nên  $\widehat{ABC}=\widehat{ACB};$  $\widehat{A}=90°$

Xét trong ∆ABC ta có:  $\widehat{ABC}+\widehat{ACB}+\widehat{A}=180°$ 

Nên  $\widehat{ABC}=\widehat{ACB}=\frac{180°-\widehat{A}}{2}=\frac{180°-90°}{2}=45°.$

Do ∆BCD vuông cân tại đỉnh B nên  $\widehat{BCD}=\widehat{BDC};$  $\widehat{CBD}=90°$

Xét trong ∆BCD ta có:  $\widehat{BCD}+\widehat{BDC}+\widehat{CBD}=180°$ 

Nên  $\widehat{BCD}=\widehat{BDC}=\frac{180°-\widehat{CBD}}{2}=\frac{180°-90°}{2}=45°.$

Ta có  $\widehat{ABC}=45°=\widehat{BCD}$ nên AB // CD (hai góc so le trong bằng nhau).

Vậy ABCD là một hình thang với AB, CD là hai đáy; cạnh bên của hình thang đó là AC vuông góc với đáy AB nên hình thang đó là hình thang vuông.

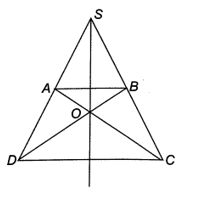
Do ABCD là hình thang cân nên AD = BC, AC = BD,   $\widehat{ADC}=\widehat{BCD}$

Xét ∆ABC và ∆BAD có

BC = AD, AC = BD, cạnh AB chung

Do đó ∆ABC = ∆BAD (c.c.c)

Suy ra  $\widehat{BAC}=\widehat{ABD}$.

Từ đó OAB là tam giác cân tại O, nên OA = OB.

Ta có: OA + OC = AC; OB + OD = BD, mà OA = OB, AC = BD

Suy ra OC = OD.

Do đó O cách đều A và B; O cách đều C và D;

Do AB // CD nên  $\widehat{SAB}=\widehat{SDC}$;  $\widehat{SBA}=\widehat{SCD}$ (các cặp góc ở vị trí đồng vị)

Mà  $\widehat{ADC}=\widehat{BCD}$ hay  $\widehat{SDC}=\widehat{SCD}$ suy ra  $\widehat{SAB}=\widehat{SDC}=\widehat{SBA}=\widehat{SCD}$

Suy ra SAB, SCD là các tam giác cân tại đỉnh S nên SA = SB, SC = SD

Do đó S cũng cách đều A và B, cách đều C và D.

Vậy S và O cùng nằm trên đường trung trực của AB, của CD nên đường thẳng SO đi qua trung điểm của AB, CD.

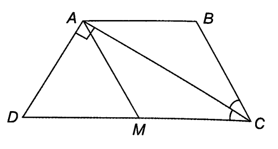
Do CA là tia phân giác của  $\widehat{C}$ nên  $\widehat{BCA}=\widehat{ACD}$

Mà ABCD là hình thang cân nên AB // CD, suy ra  $\widehat{BAC}=\widehat{ACD}$ (hai góc so le trong)

Do đó,  $\widehat{BAC}=\widehat{BCA}$, suy ra ∆ABC cân tại B.

Đặt  $\widehat{BAC}=\alpha$ thì  $\widehat{C}=2\alpha$.

Vì ABCD là hình thang cân nên  $\widehat{D}=\widehat{C}=2\alpha .$

Tam giác ADC vuông tại A nên  $\widehat{ADC}+\widehat{ACD}=2\alpha +\alpha =90°,$ suy ra  $\alpha =30°,\widehat{D}=60°.$

Lấy điểm M thuộc cạnh huyền DC sao cho DM = AD, mà  $\widehat{D}=60°$ thì AMD là tam giác đều, nên  $\widehat{MAD}=60°$

Khi đó  $\widehat{MAC}=\widehat{CAD}-\widehat{MAD}=90°-60°=30°$

Suy ra  $\widehat{ACM}=\widehat{CAM}=30°$ nên tam giác MAC cân tại M

Do đó AM = MC, mà AM = DM = AD

Nên AM = DM = AD = MC hay DC = 2AD.

Vậy AB = BC = AD, DC = 2AD nên chu vi hình thang bằng

AB + BC + CD + AD = 5AD = 5.2 = 10 cm.