Câu hỏi:

27/07/2023 3,359

Cho tam giác ABC vuông cân tại đỉnh A. Ghép thêm vào phía ngoài tam giác đó tam giác BCD vuông cân tại đỉnh B.

Chứng minh tứ giác ABDC là một hình thang vuông (hình thang có một cạnh bên vuông góc với hai đáy).

Xem lời giải

Câu hỏi trong đề: Giải SBT Toán 8 KNTT Bài 11: Hình thang cân có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

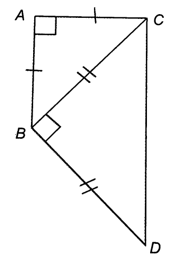
Media VietJack

Do ∆ABC vuông cân tại đỉnh A nên $\hat{A B C} = \hat{A C B};$ $\hat{A} = 90 °$

Xét trong ∆ABC ta có: $\hat{A B C} + \hat{A C B} + \hat{A} = 180 °$

Nên $\hat{A B C} = \hat{A C B} = \frac{180 ° - \hat{A}}{2} = \frac{180 ° - 90 °}{2} = 45 ° .$

Do ∆BCD vuông cân tại đỉnh B nên $\hat{B C D} = \hat{B D C};$ $\hat{C B D} = 90 °$

Xét trong ∆BCD ta có: $\hat{B C D} + \hat{B D C} + \hat{C B D} = 180 °$

Nên $\hat{B C D} = \hat{B D C} = \frac{180 ° - \hat{C B D}}{2} = \frac{180 ° - 90 °}{2} = 45 ° .$

Ta có $\hat{A B C} = 45 ° = \hat{B C D}$ nên AB // CD (hai góc so le trong bằng nhau).

Vậy ABCD là một hình thang với AB, CD là hai đáy; cạnh bên của hình thang đó là AC vuông góc với đáy AB nên hình thang đó là hình thang vuông.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tính các góc của hình thang ABCD (AB, CD là hai đáy) biết $\hat{A} = 2 \hat{D}$ , $\hat{B} = \hat{C} + 40 ° .$

Xem đáp án

Lời giải

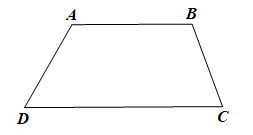
Media VietJack

Trong hình thang ABCD có:

$\hat{A}$ và $\hat{D}$ là 2 góc bù nhau, $\hat{B}$ và $\hat{C}$ là 2 góc bù nhau.

Do đó $\hat{A} + \hat{D} = 180 °$ , $\hat{B} + \hat{C} = 180 °$

Mà $\hat{A} = 2 \hat{D}$ nên $2 \hat{D} + \hat{D} = 180 °$ , suy ra $\hat{D} = 60 °$ . Do đó $\hat{A} = 2 \hat{D} = 2 \cdot 60 ° = 120 ° .$

$\hat{B} = \hat{C} + 40 °$ nên $\hat{C} + 40 ° + \hat{C} = 180 °$ , hay $2 \hat{C} = 140 °$ , suy ra $\hat{C} = 70 °$

Do đó $\hat{B} = \hat{C} + 40 ° = 70 ° + 40 ° = 110 °$

Vậy hình thang ABCD có $\hat{A} = 120 °; \hat{B} = 110 °; \hat{C} = 70 °; \hat{D} = 60 ° .$

Câu 2

Cho hình thang cân ABCD với hai đáy AB và CD, đường chéo AC vuông góc với cạnh bên AD, tia CA là tia phân giác của góc C.

Tính chu vi của hình thang đó biết rằng AD = 2 cm.

Xem đáp án

Lời giải

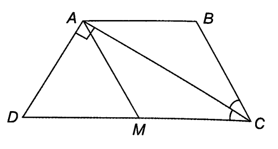
Media VietJack

Do CA là tia phân giác của $\hat{C}$ nên $\hat{B C A} = \hat{A C D}$

Mà ABCD là hình thang cân nên AB // CD, suy ra $\hat{B A C} = \hat{A C D}$ (hai góc so le trong)

Do đó, $\hat{B A C} = \hat{B C A}$ , suy ra ∆ABC cân tại B.

Đặt $\hat{B A C} = α$ thì $\hat{C} = 2 α$ .

Vì ABCD là hình thang cân nên $\hat{D} = \hat{C} = 2 α .$

Tam giác ADC vuông tại A nên $\hat{A D C} + \hat{A C D} = 2 α + α = 90 °,$ suy ra $α = 30 °, \hat{D} = 60 ° .$

Lấy điểm M thuộc cạnh huyền DC sao cho DM = AD, mà $\hat{D} = 60 °$ thì AMD là tam giác đều, nên $\hat{M A D} = 60 °$

Khi đó $\hat{M A C} = \hat{C A D} - \hat{M A D} = 90 ° - 60 ° = 30 °$

Suy ra $\hat{A C M} = \hat{C A M} = 30 °$ nên tam giác MAC cân tại M

Do đó AM = MC, mà AM = DM = AD

Nên AM = DM = AD = MC hay DC = 2AD.

Vậy AB = BC = AD, DC = 2AD nên chu vi hình thang bằng

AB + BC + CD + AD = 5AD = 5.2 = 10 cm.

Câu 3

Cho hình thang cân ABCD với hai đường thẳng chứa hai cạnh bên AD, BC cắt nhau tại S. Gọi O là giao điểm của hai đường chéo AC và BD. Chứng minh đường thẳng SO đi qua trung điểm của AB, đi qua trung điểm của CD.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Chứng minh rằng trong hình thang có nhiều nhất hai góc tù.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Cho tam giác ABC vuông cân tại đỉnh A. Ghép thêm vào phía ngoài tam giác đó tam giác BCD vuông cân tại đỉnh B. Chứng minh tứ giác ABDC là một hình thang vuông (hình thang có một cạnh bên vuông góc với hai đáy).

Bình luận

Tính các góc của hình thang ABCD (AB, CD là hai đáy) biết A^=2D^, B^=C^+40°.

Cho hình thang cân ABCD với hai đáy AB và CD, đường chéo AC vuông góc với cạnh bên AD, tia CA là tia phân giác của góc C. Tính chu vi của hình thang đó biết rằng AD = 2 cm.

Cho hình thang cân ABCD với hai đường thẳng chứa hai cạnh bên AD, BC cắt nhau tại S. Gọi O là giao điểm của hai đường chéo AC và BD. Chứng minh đường thẳng SO đi qua trung điểm của AB, đi qua trung điểm của CD.

Chứng minh rằng trong hình thang có nhiều nhất hai góc tù.

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho tam giác ABC vuông cân tại đỉnh A. Ghép thêm vào phía ngoài tam giác đó tam giác BCD vuông cân tại đỉnh B.

Chứng minh tứ giác ABDC là một hình thang vuông (hình thang có một cạnh bên vuông góc với hai đáy).

Tính các góc của hình thang ABCD (AB, CD là hai đáy) biết $\hat{A} = 2 \hat{D}$ , $\hat{B} = \hat{C} + 40 ° .$

Cho hình thang cân ABCD với hai đáy AB và CD, đường chéo AC vuông góc với cạnh bên AD, tia CA là tia phân giác của góc C.

Tính chu vi của hình thang đó biết rằng AD = 2 cm.