Giải SBT Toán 8 KNTT Bài 13: Hình chữ nhật có đáp án

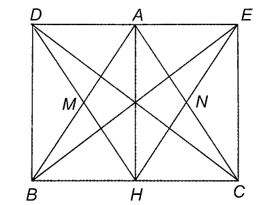
a) • Tứ giác AHBD có M là trung điểm của AB và HD nên là hình bình hành.

Do AH là đường cao của ∆ABC nên AH ⊥ BC, suy ra  $\widehat{AHB}=90°$

Hình bình hành AHBD có  $\widehat{AHB}=90°$ nên AHBD là hình chữ nhật.

• Tương tự, tứ giác AHCE có N là trung điểm của AC và HE nên là hình bình hành.

Lại có  $\widehat{AHC}=90°$ nên AHCE là hình chữ nhật.

• Do AHBD, AHCE là các hình chữ nhật (chứng minh trên)

Suy ra  $\widehat{ADB}=\widehat{DBH}=\widehat{HCE}=\widehat{AEC}=90°$

Tứ giác BCED có  $\widehat{ADB}=\widehat{DBH}=\widehat{HCE}=\widehat{AEC}=90°$ là các góc ở đỉnh nên BCED là hình chữ nhật. 

b) Vì ADBH, AECH là các hình chữ nhật nên AD = BH, AE = HC, AD // BC, AE // BC

Mà ∆ABC cân tại A có AH là đường cao nên đồng thời là đường trung tuyến, do đó H là trung điểm của BC, suy ra BH = HC.

Từ đó, AD = BH = HC = AE

Tứ giác ADHC có: AD // HC, AD = HC nên ADHC là hình bình hành.

Tứ giác ABHE có: AE // BH, AE = BH nên ABHE là hình bình hành

Vì ADHC là hình bình hành nên CD cắt AH tại trung điểm của AH.

Vì AEHB là hình bình hành nên BE cắt AH tại trung điểm của AH.

Vậy giao điểm của BE và CD là trung điểm của AH.

c) Do AHBD, AHCE là các hình chữ nhật nên AB = DH, AC = HE (hai đường chéo bằng nhau).

Mà AB = AC (do ∆ABC cân tại A) nên DH = HE.

Do BCED là hình chữ nhật (chứng minh câu a) nên CD = BE (hai đường chéo bằng nhau).

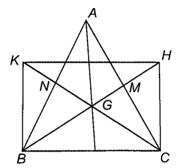
Vì BM, CN là trung tuyến của ∆ABC nên M, N lần lượt là trung điểm của AC, AB.

Do M là trung điểm của AC và của GH nên AGCH là hình bình hành

Từ đó HC = AG và HC // AG. (1)

Do N là trung điểm của AB và của GK nên AGBK là hình bình hành

Suy ra KB = AG và KB // AG. (2)

Từ (1) và (2) suy ra BK = CH và BK // CH.

Tứ giác BCHK có hai cạnh đối BK, CH bằng nhau và song song nên là một hình bình hành.

Vì tam giác ABC cân tại A nên trung tuyến AG là đường cao tức AG ⊥ BC hay KB ⊥ BC, suy ra BCHK là hình chữ nhật.

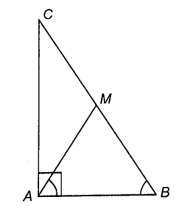
a) Cho tam giác ABC vuông tại A. Do B là góc nhọn, có điểm M thuộc BC sao cho  $\widehat{BAM}=\widehat{ABM}$; tam giác ABM cân tại M nên MA = MB.

Do  $\widehat{BAM}+\widehat{MAC}=\widehat{ABM}+\widehat{ACM}=90°$ nên suy ra  $\widehat{MAC}=\widehat{ACM}$, do đó tam giác ACM cân tại M tức là MA = MC.

Vậy  $MA=MB=MC=\frac{1}{2}BC$.

b) Ngược lại, nếu có M thuộc BC sao cho  $MA=MB=MC=\frac{1}{2}BC$ thì tam giác MAB cân tại M, tam giác MAC cân tại M, suy ra  $\widehat{MAB}=\widehat{B};\widehat{MAC}=\widehat{C}$

Ta có:  $\widehat{A}=\widehat{MAC}+\widehat{MAB}$

Nên  $\widehat{A}=\widehat{B}+\widehat{C}$ mà  $\widehat{A}+\widehat{B}+\widehat{C}=180°$ nên  $\widehat{A}=90°$.

Vậy tam giác ABC vuông tại A.