Giải SGK Toán 8 KNTT Bài 34. Ba trường hợp đồng dạng của hai tam giác có đáp án
133 người thi tuần này 4.6 1.2 K lượt thi 22 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 06
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 05
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 04
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 03
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 02
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 01
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức có đáp án - Đề 10
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức có đáp án - Đề 9
Danh sách câu hỏi:
Lời giải
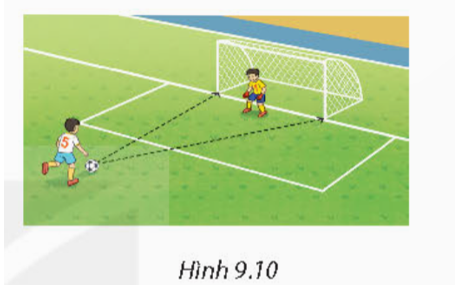
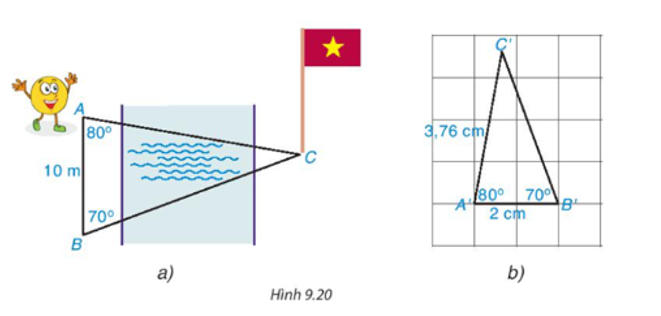
Vì trong hình vẽ mặt sân được vẽ nghiêng nên nếu đo trực tiếp trong sách giáo khoa sẽ không đúng bằng góc thực tế.
Vẽ một tam giác bằng dụng cụ học tập trên giấy có một góc đúng bằng góc sút. Từ đó sử dụng dụng cụ học tập là thước đo góc để đo góc sút.
Lời giải
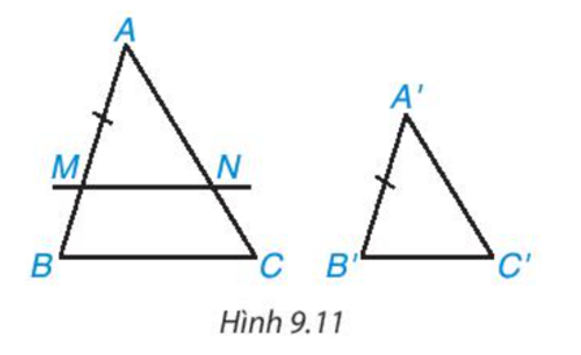
a) Nếu A′B′ = AB thì từ , suy ra A′C′ = AC và B′C′ = BC.
Do đó ΔABC = ΔA'B'C' (c.c.c). Vậy ΔABC ∽ ΔA'B'C'.
Lời giải
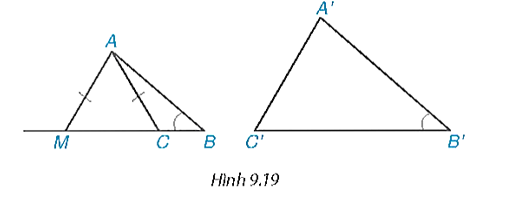
b) Ta có MN // BC ( M ∈ AB, N ∈ AC). Suy ra ΔAMN ∽ ΔABC.
Suy ra .
Mà nên .
Có AM = A'B', suy ra A'C' = AN và B'C' = MN nên ∆AMN = ∆A'B'C' (c.c.c).
Suy ra ∆AMN ∽ ∆A'B'C', mà ∆AMN ∽ ∆ABC nên ∆ABC ∽ ∆A'B'C'.
Lời giải
c) Nếu A'B' > AB, bằng cách đổi vai trò cho ∆ABC và ∆A'B'C' cho nhau thì theo câu b), ta có ∆ABC ∽ ∆A'B'C'.
Lời giải
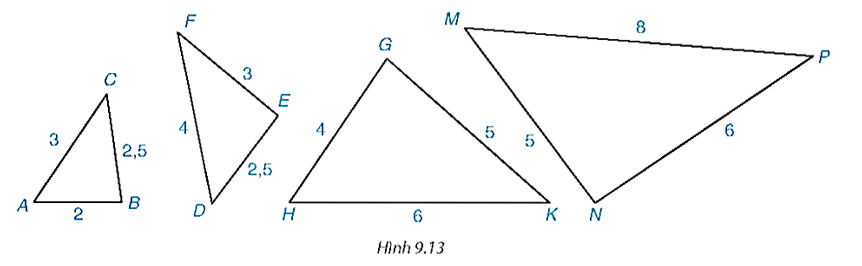
Ta có ∆ABC ∽ ∆HGK (c.c.c) vì .
Ta có ∆DEF ∽ ∆MNP (c.c.c) vì .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.