Câu hỏi:
29/10/2023 505
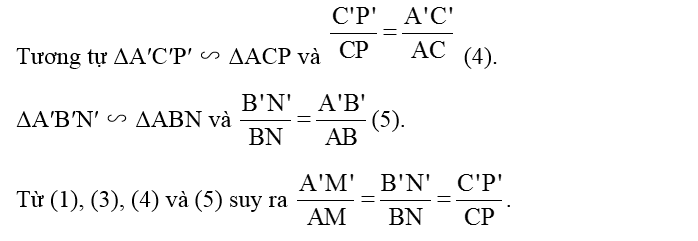
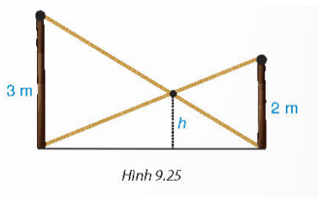
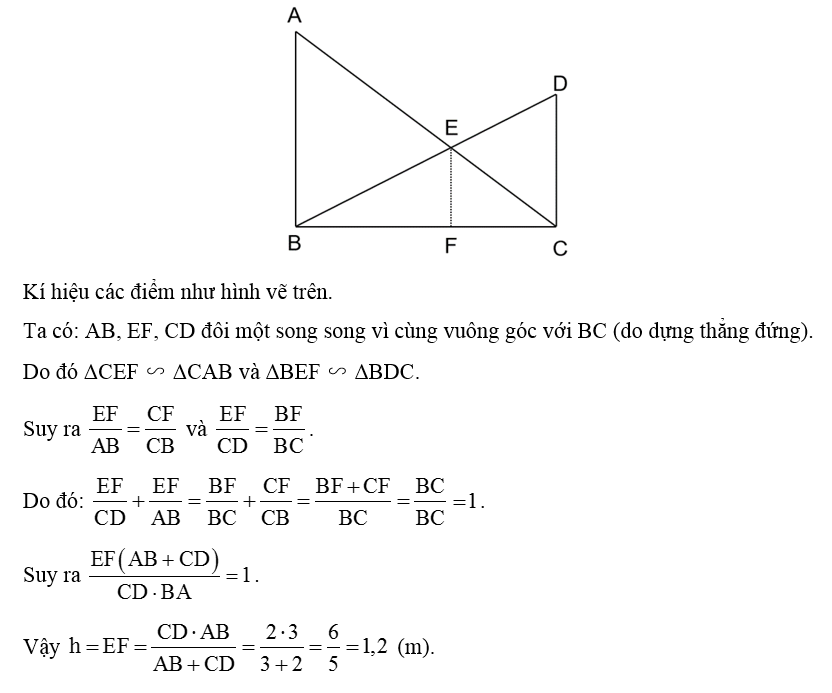
Bạn Tròn đang đứng ở vị trí điểm A bên bờ sông và nhờ anh Pi tính giúp khoảng cách từ chỗ mình đứng đến chân một cột cờ tại điểm C bên kia sông (H.9.20a). Anh Pi lấy một vị trí B sao cho AB = 10 m, và vẽ một tam giác A'B'C' trên giấy với A′B′ = 2 cm, .(H.9.20b).
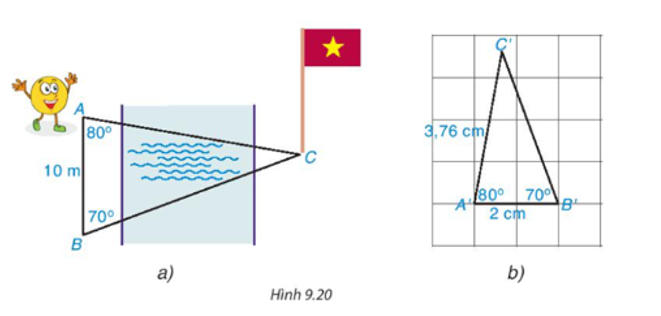
Em hãy dự đoán xem tam giác A'B'C' có đồng dạng với tam giác ABC không. Nếu có thì tỉ số đồng dạng là bao nhiêu?
Bạn Tròn đang đứng ở vị trí điểm A bên bờ sông và nhờ anh Pi tính giúp khoảng cách từ chỗ mình đứng đến chân một cột cờ tại điểm C bên kia sông (H.9.20a). Anh Pi lấy một vị trí B sao cho AB = 10 m, và vẽ một tam giác A'B'C' trên giấy với A′B′ = 2 cm, .(H.9.20b).
Em hãy dự đoán xem tam giác A'B'C' có đồng dạng với tam giác ABC không. Nếu có thì tỉ số đồng dạng là bao nhiêu?
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Dự đoán: Hai tam giác có hình dạng rất giống nhau chỉ khác về kích thước nên chúng có khả năng đồng dạng với nhau. Khi đó tỉ số đồng dạng bằng .
(AB = 10 m = 1 000 cm, A'B' = 2 cm)
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho AM, BN, CP là các đường trung tuyến của tam giác ABC. Cho A'M', B'N', C'P' là các đường trung tuyến của tam giác A'B'C'. Biết rằng ΔA′B′C′ ∽ ΔABC.
Chứng minh rằng .
Cho AM, BN, CP là các đường trung tuyến của tam giác ABC. Cho A'M', B'N', C'P' là các đường trung tuyến của tam giác A'B'C'. Biết rằng ΔA′B′C′ ∽ ΔABC.
Chứng minh rằng .
Xem đáp án »
29/10/2023
5,651
Câu 2:
Có hai chiếc cột dựng thẳng đứng trên mặt đất với chiều cao lần lượt là 3 m và 2 m. Người ta nối hai sợi dây từ đỉnh cột này đến chân cột kia và hai sợi dây cắt nhau tại một điểm (H.9.25). Hãy tính độ cao h của điểm đó so với mặt đất.
Có hai chiếc cột dựng thẳng đứng trên mặt đất với chiều cao lần lượt là 3 m và 2 m. Người ta nối hai sợi dây từ đỉnh cột này đến chân cột kia và hai sợi dây cắt nhau tại một điểm (H.9.25). Hãy tính độ cao h của điểm đó so với mặt đất.
Xem đáp án »
29/10/2023
3,745
Câu 3:
Cho tam giác ABC có AB = 12 cm, AC = 15 cm. Trên các tia AB, AC lần lượt lấy các điểm M, N sao cho AM = 10 cm, AN = 8 cm. Chứng minh rằng ΔABC ∽ ΔANM.
Cho tam giác ABC có AB = 12 cm, AC = 15 cm. Trên các tia AB, AC lần lượt lấy các điểm M, N sao cho AM = 10 cm, AN = 8 cm. Chứng minh rằng ΔABC ∽ ΔANM.
Xem đáp án »
29/10/2023
3,057
Câu 4:
Cho hai tam giác đồng dạng. Tam giác thứ nhất có độ dài ba cạnh là 4 cm, 8 cm và 10 cm. Tam giác thứ hai có chu vi là 33 cm. Độ dài ba cạnh của tam giác thứ hai là bộ ba nào sau đây?
a) 6 cm, 12 cm, 15 cm. b) 8 cm, 16 cm, 20 cm.
c) 6 cm, 9 cm, 18 cm. d) 8 cm, 10 cm, 15 cm.
Cho hai tam giác đồng dạng. Tam giác thứ nhất có độ dài ba cạnh là 4 cm, 8 cm và 10 cm. Tam giác thứ hai có chu vi là 33 cm. Độ dài ba cạnh của tam giác thứ hai là bộ ba nào sau đây?
a) 6 cm, 12 cm, 15 cm. b) 8 cm, 16 cm, 20 cm.
c) 6 cm, 9 cm, 18 cm. d) 8 cm, 10 cm, 15 cm.
Xem đáp án »
29/10/2023
2,931
Câu 5:
Cho tam giác ABC có chu vi bằng 18 cm và tam giác DEF có chu vi bằng 27 cm. Biết rằng AB = 4 cm, BC = 6 cm, DE = 6 cm, FD = 12 cm. Chứng minh ΔABC ∽ ΔDEF.
Cho tam giác ABC có chu vi bằng 18 cm và tam giác DEF có chu vi bằng 27 cm. Biết rằng AB = 4 cm, BC = 6 cm, DE = 6 cm, FD = 12 cm. Chứng minh ΔABC ∽ ΔDEF.
Xem đáp án »
29/10/2023
2,414
Câu 6:
Cho ΔA'B'C' ∽ ΔABC. Trên tia đối của các tia CB, C'B' lần lượt lấy các điểm M, M' sao cho . Chứng minh rằng ΔA'B'M' ∽ ΔABM.
Cho ΔA'B'C' ∽ ΔABC. Trên tia đối của các tia CB, C'B' lần lượt lấy các điểm M, M' sao cho . Chứng minh rằng ΔA'B'M' ∽ ΔABM.
Xem đáp án »
29/10/2023
1,811
Câu 7:
Cho góc BAC và các điểm M, N lần lượt trên các đoạn thẳng AB, AC sao cho .
a) Chứng minh rằng ΔABN ∽ ΔACM.
Cho góc BAC và các điểm M, N lần lượt trên các đoạn thẳng AB, AC sao cho .
a) Chứng minh rằng ΔABN ∽ ΔACM.
Xem đáp án »
29/10/2023
1,648
về câu hỏi!