Giải VTH Toán 8 KNTT Bài 33. Hai tam giác đồng dạng có đáp án

39 người thi tuần này 4.6 421 lượt thi 8 câu hỏi

Câu 1/8

Chọn phương án đúng.

Cho ∆ABC ᔕ ∆MNP với tỉ số đồng dạng bằng 2, trong đó tam giác ABC không cân. Khẳng định nào sau đây là đúng?

A. AB = 2NP.

B. $\hat{A} = 2 \hat{M} .$

C. BC = 2NP.

D. MN = 2AB.

Xem đáp án

Lời giải

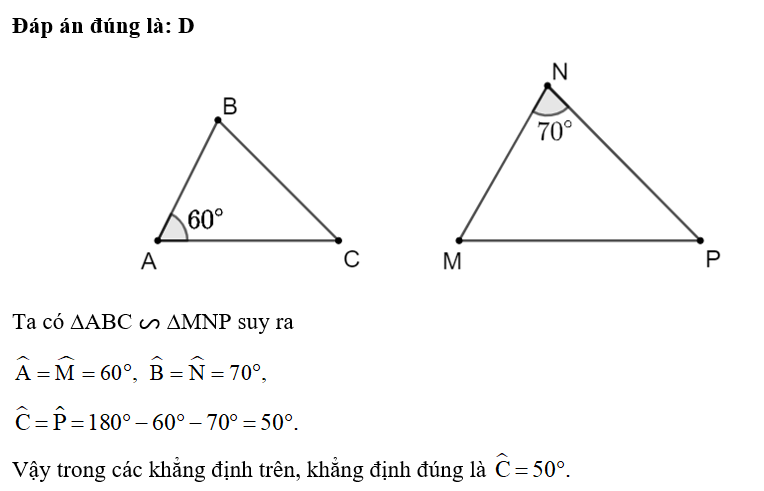
Đáp án đúng là: C

Ta có ∆ABC ᔕ ∆MNP suy ra $\hat{A} = \hat{M}, \hat{B} = \hat{N}, \hat{C} = \hat{P} .$

Vì ∆ABC ᔕ ∆MNP với tỉ số đồng dạng bằng 2 nên ta có

AB = 2MN, AC = 2MP, BC = 2NP.

Câu 2/8

Chọn phương án đúng.

Cho ∆ABC ᔕ ∆MNP. Biết $\hat{A} = 60 °, \hat{N} = 70 ° .$ Khẳng định nào sau đây là đúng?

A. $\hat{P} = 60 ° .$

B. $\hat{B} = 50 ° .$

C. $\hat{M} = 50 ° .$

D. $\hat{C} = 50 ° .$

Xem đáp án

Lời giải

Chọn phương án đúng. Cho ∆ABC ᔕ ∆MNP. (ảnh 1)

Câu 3/8

Cho ∆ABC ᔕ ∆MNP, khẳng định nào sau đây không đúng?

a) ∆MNP ᔕ ∆ABC.

b) ∆BCA ᔕ ∆NPM.

c) ∆CBA ᔕ ∆PMN.

d) ∆ACB ᔕ ∆MNP.

Xem đáp án

Lời giải

Từ giả thiết ta thấy ∆ABC ᔕ ∆MNP với các cặp đỉnh tương ứng: (A, M), (B, N), (C, P). Do đó các khẳng định a), b), c) đúng và khẳng định d) không đúng.

Câu 4/8

Những khẳng định nào sau đây là đúng?

a) Hai tam giác bằng nhau thì đồng dạng với nhau.

b) Hai tam giác bất kì đồng dạng với nhau.

c) Hai tam giác đều bất kì đồng dạng với nhau.

d) Hai tam giác vuông bất kì đồng dạng với nhau.

e) Hai tam giác đồng dạng thì bằng nhau.

Xem đáp án

Lời giải

Khẳng định a và c đúng. Khẳng định b, d và e sai.

Câu 5/8

Trong Hình 9.1, ABC là tam giác không cân; M, N, P lần lượt là trung điểm của BC, CA, AB. Hãy tìm trong hình năm tam giác khác nhau mà chúng đôi một đồng dạng với nhau. Giải thích vì sao chúng đồng dạng.

Xem đáp án

Lời giải

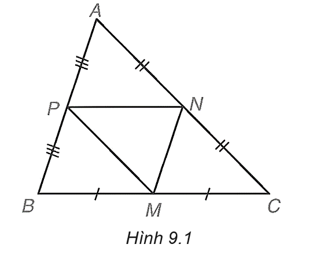
Xét hai tam giác APN và MNP, ta có:

$\hat{A P N} = \hat{M N P}, \hat{A N P} = \hat{M P N}$ (các góc tương ứng), PN là cạnh chung.

Vậy $Δ A P N = Δ M N P$ (g.g). Tương tự $Δ P B M = Δ M N P, Δ N M C = Δ M N P .$

Do PN là đường trung bình của tam giác ABC nên PN // BC.

Suy ra ∆APN ᔕ ∆ABC.

Vậy bốn tam giác APN, PBM, NMC, MNP đôi một bằng nhau và cùng đồng dạng với tam giác ABC. Do đó cả năm tam giác này đôi một đồng dạng với nhau.

Câu 6/8

Cho tam giác ABC cân tại đỉnh A và tam giác MNP cân tại đỉnh M. Biết rằng $\hat{B A C} = \hat{P M N},$ AB = 2MN. Chứng minh ∆MNP ᔕ ∆ABC và tìm tỉ số đồng dạng.

Xem đáp án

Lời giải

Cho tam giác ABC cân tại đỉnh A và tam giác MNP cân tại đỉnh M. (ảnh 1)

Cho tam giác ABC cân tại đỉnh A và tam giác MNP cân tại đỉnh M. (ảnh 2)

Câu 7/8

Cho ∆ABC ᔕ ∆MNP. Biết rằng $6 \hat{A} = 2 \hat{N} = 3 \hat{C} .$ Hãy tính số đo các góc của hai tam giác ABC và MNP.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 8/8

Cho ∆ABC ᔕ ∆DEF với tỉ số đồng dạng bằng 2. Biết rằng AB = 4 cm, EF = 3 cm và tổng chu vi của hai tam giác bằng 27 cm. Hãy tính độ dài các cạnh BC, CA, DE, FD của hai tam giác trên.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem tiếp với tài khoản VIP

Còn 2/8 câu hỏi, đáp án và lời giải chi tiết.

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Ôn vào 10

Ôn vào 6

ĐGNL-ĐGTD

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Toán

Toán

Toán

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Khoa học tự nhiên

Tin học

Lịch sử

Địa lí

Toán

Toán

Toán

Toán

Tiếng Việt

Tiếng Anh

Giải VTH Toán 8 KNTT Bài 33. Hai tam giác đồng dạng có đáp án

🔥 Học sinh cũng đã học

Bài tập Bài toán thực tiễn liên quan đến thể tích, diện tích xung quanh của hình chóp tứ giác đều lớp 8 (có lời giải)

Bài tập Tính diện tích xung quanh và thể tích của hình chóp tứ giác đều lớp 8 (có lời giải)

Bài tập Bài toán thực tiễn liên quan đến tính thể tích, diện tích xung quanh của hình chóp tam giác đều lớp 8 (có lời giải)

Bài tập Tính diện tích xung quanh và thể tích của hình chóp tam giác đều lớp 8 (có lời giải)

Bài tập Các bài toán thực tiễn gắn với việc vận dụng các tam giác vuông đồng dạng lớp 8 (có lời giải)

Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore lớp 8 (có lời giải)

Bài tập Chứng minh các tính chất hình học lớp 8 (có lời giải)

Bài tập Tính độ dài cạnh trong tam giác vuông bằng cách sử dụng định lí Pythagore lớp 8 (có lời giải)

Danh sách câu hỏi:

Chọn phương án đúng. Cho ∆ABC ᔕ ∆MNP với tỉ số đồng dạng bằng 2, trong đó tam giác ABC không cân. Khẳng định nào sau đây là đúng? A. AB = 2NP. B. A^=2M^. C. BC = 2NP. D. MN = 2AB.

Chọn phương án đúng. Cho ∆ABC ᔕ ∆MNP. Biết A^=60°,N^=70°. Khẳng định nào sau đây là đúng? A. P^=60°. B. B^=50°. C. M^=50°. D. C^=50°.

Cho ∆ABC ᔕ ∆MNP, khẳng định nào sau đây không đúng? a) ∆MNP ᔕ ∆ABC. b) ∆BCA ᔕ ∆NPM. c) ∆CBA ᔕ ∆PMN. d) ∆ACB ᔕ ∆MNP.

Trong Hình 9.1, ABC là tam giác không cân; M, N, P lần lượt là trung điểm của BC, CA, AB. Hãy tìm trong hình năm tam giác khác nhau mà chúng đôi một đồng dạng với nhau. Giải thích vì sao chúng đồng dạng.

Cho tam giác ABC cân tại đỉnh A và tam giác MNP cân tại đỉnh M. Biết rằng BAC^=PMN^, AB = 2MN. Chứng minh ∆MNP ᔕ ∆ABC và tìm tỉ số đồng dạng.

Cho ∆ABC ᔕ ∆MNP. Biết rằng 6A^=2N^=3C^. Hãy tính số đo các góc của hai tam giác ABC và MNP.

Cho ∆ABC ᔕ ∆DEF với tỉ số đồng dạng bằng 2. Biết rằng AB = 4 cm, EF = 3 cm và tổng chu vi của hai tam giác bằng 27 cm. Hãy tính độ dài các cạnh BC, CA, DE, FD của hai tam giác trên.

Xem tiếp với tài khoản VIP

Đăng ký

Đăng nhập

Quên mật khẩu

CHỌN BỘ SÁCH BẠN MUỐN XEM

Chọn phương án đúng.

Cho ∆ABC ᔕ ∆MNP với tỉ số đồng dạng bằng 2, trong đó tam giác ABC không cân. Khẳng định nào sau đây là đúng?

A. AB = 2NP.

B. $\hat{A} = 2 \hat{M} .$

C. BC = 2NP.

D. MN = 2AB.

Chọn phương án đúng.

Cho ∆ABC ᔕ ∆MNP. Biết $\hat{A} = 60 °, \hat{N} = 70 ° .$ Khẳng định nào sau đây là đúng?

A. $\hat{P} = 60 ° .$

B. $\hat{B} = 50 ° .$

C. $\hat{M} = 50 ° .$

D. $\hat{C} = 50 ° .$

Cho ∆ABC ᔕ ∆MNP, khẳng định nào sau đây không đúng?

a) ∆MNP ᔕ ∆ABC.

b) ∆BCA ᔕ ∆NPM.

c) ∆CBA ᔕ ∆PMN.

d) ∆ACB ᔕ ∆MNP.

Cho tam giác ABC cân tại đỉnh A và tam giác MNP cân tại đỉnh M. Biết rằng $\hat{B A C} = \hat{P M N},$ AB = 2MN. Chứng minh ∆MNP ᔕ ∆ABC và tìm tỉ số đồng dạng.

Cho ∆ABC ᔕ ∆MNP. Biết rằng $6 \hat{A} = 2 \hat{N} = 3 \hat{C} .$ Hãy tính số đo các góc của hai tam giác ABC và MNP.