Giải SGK Toán 8 KNTT Bài 35. Định lí Pythagore và ứng dụng có đáp án

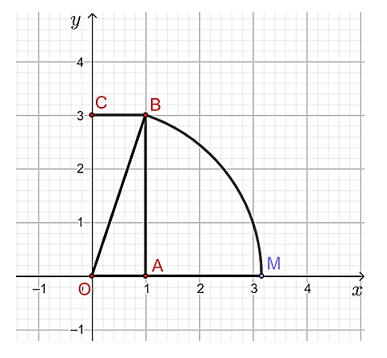
Để biết được điểm M biểu diễn số thực nào, ta cần tính độ dài đoạn thẳng OM, hay chính là tính độ dài đường chéo OB của hình chữ nhật OABC khi biết chiều dài và chiều rộng của hình chữ nhật đó, điều này dẫn đến việc cần tính độ dài cạnh huyền của tam giác vuông khi biết độ dài hai cạnh góc vuông. Để làm được điều này, ta sẽ sử dụng kiến thức của bài học hôm nay.

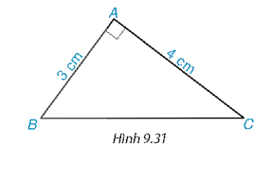
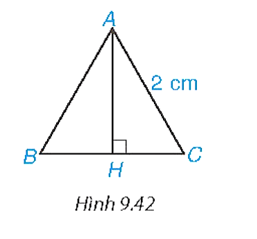
+ Đo độ dài BC ta được BC = 5 cm, vậy BC² = 25.

+ Ta có AB² = 3² = 9; AC² = 4² = 16. Vậy AB² + AC² = 25.

Vậy AB² + AC² = BC².

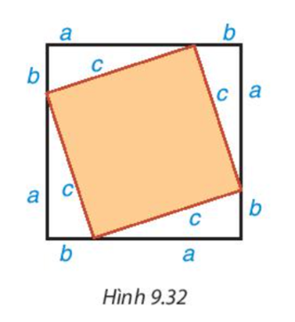
+ Phần bìa bị che lấp là hình vuông cạnh c. Diện tích của hình vuông là c².

+ Tổng diện tích bốn tam giác vuông: 4.$\frac{1}{2}$.a.b = 2ab.

+ Diện tích tấm bìa hình vuông có cạnh bằng a + b là: (a + b)².

+ Khi đó (a + b)² = c² + 2ab, tức là a² + 2ab + b² = c² + 2ab. Suy ra c² = a² + b².

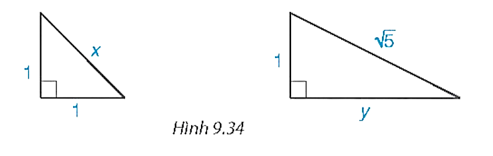
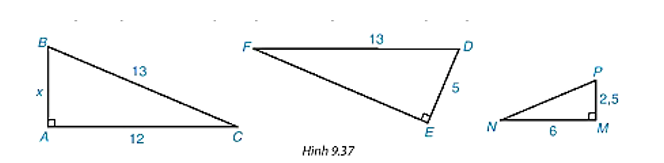
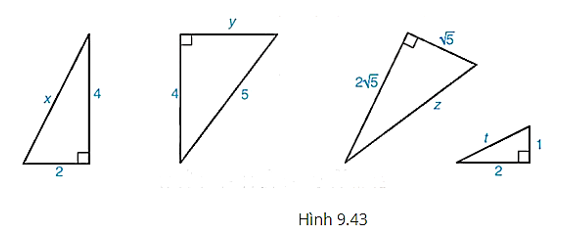
+ Theo định lí Pythagore ta có: x² = 1² + 1² = 2. Suy ra $x=\sqrt{2}$.

+ Theo định lí Pythagore ta có: 5 = 1² + y². Suy ra y² = 5 – 1 = 4. Suy ra y = 2.

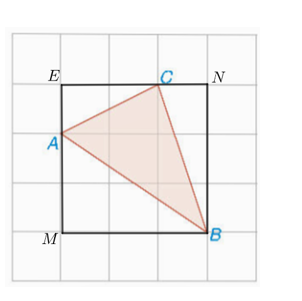
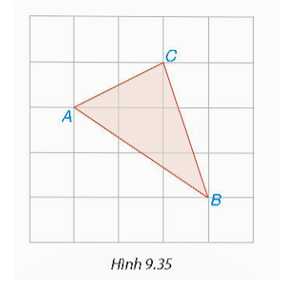
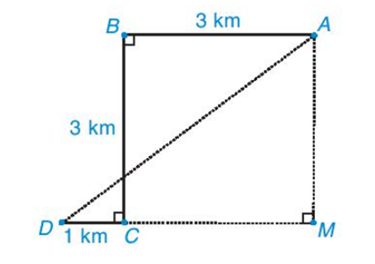
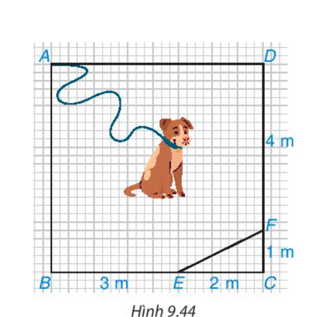
Từ A kẻ AM sao cho AM ⊥ MB như hình vẽ trên.

Từ C kẻ CN sao cho CN ⊥ NB như hình vẽ trên.

Từ C kẻ EC sao cho EC ⊥ EA như hình vẽ trên.

- Xét ΔAMB có AM ⊥ MB 

Suy ra ΔAMB là tam giác vuông tại M.

Ta có: AB² = AM² + MB² (định lí Pythagore).

Khi đó AB² = 2² + 3² = 13. Suy ra AB = $\sqrt{13}$ cm.

- Xét ΔBNC có CN ⊥ NB

Suy ra ΔBNC là tam giác vuông tại N.

Ta có: BC² = NB² + NC² (định lí Pythagore).

Khi đó BC² = 3² + 1² = 10. Suy ra BC = $\sqrt{10}$ cm.

- Xét ΔAEC có EC ⊥ EA.

Suy ra ΔAEC là tam giác vuông tại E

Ta có: AC² = AE² + EC² (định lí Pythagore).

Khi đó AC² = 1² + 2² = 5. Suy ra AC = $\sqrt{5}$ cm.

Nếu điểm M biểu diễn cho số thực x thì đoạn thẳng OM có độ dài x (đơn vị độ dài).

Đoạn thẳng OM là cạnh huyền của một tam giác vuông với hai cạnh góc vuông là hai cạnh của hình chữ nhật.Theo định lí Pythagore ta có x² = 1² + 3² = 10. Suy ra $x=\sqrt{10}$.

Vậy điểm M biểu diễn số thực $\sqrt{10}$.

Tam giác ABC vuông tại A nên theo định lí Pythagore ta có: AB² + AC² = BC².

Hay x² + 12² = 13². Suy ra x² =13² – 12² = 25. Suy ra x = 5.

Vậy ∆ABC = ∆EDF (cạnh huyền – cạnh góc vuông).

Khi đó ∆ABC ∽ ∆EDF. (1)

Lại có $\frac{AB}{MP}=\frac{AC}{MN}=2;\widehat{BAC}=\widehat{NMP}=90°$.

Do đó: ∆ABC ∽ ∆MPN (c.g.c). (2)

Từ (1) và (2) suy ra ∆MPN ∽ ∆EDF.

Có BC = AM = AB = CM = 3 km (do AMCB là hình vuông).

Suy ra MD = CM + CD = 3 + 1 = 4 (km).

Xét tam giác AMD vuông tại M, theo định lí Pythagore, ta có:

AD² = AM² + MD² = 3² + 4² = 25. Suy ra AD = 5 km.

Vậy lúc đầu, khoảng cách từ chỗ người lái xe đến người khách là 5 km.

Áp dụng định lí Pythagore trong tam giác AHD vuông tại H có: 

AD² = AH² + HD² (1)

Áp dụng định lí Pythagore trong tam giác AHC vuông tại H có:

 AC² = AH² + HC² (2)

Áp dụng định lí Pythagore trong tam giác AHE vuông tại H có:

 AE² = AH² + HE² (3)

Vì HE > HC > HD suy ra HE² > HC² > HD². (4)

Từ (1), (2), (3), (4) suy ra: AE² > AC² > AD² ⇒ AE > AC > AD.

Vậy đoạn AE là lớn nhất, đoạn AD là nhỏ nhất.

- Xét tam giác ABC vuông tại A, có

BC² = AB² + AC² (định lí Pythagore) (1)

- Xét tam giác A'B'C' vuông tại A' có:

B′C′² = A′B′² + A′C′² (định lí Pythagore) (2)

Mà AB = A′B′, BC = B′C′ (3)

Từ (1), (2), (3) suy ra AC = A′C′.

Suy ra hai tam giác đã cho bằng nhau theo trường hợp cạnh – cạnh – cạnh.

Vì tam giác ABC là tam giác đều, AH ⊥ BC nên H là trung điểm của BC, suy ra

HB = HC = $\frac{BC}{2}=\frac{2}{2}=1$ (cm).

Áp đụng định lí Pythagore trong tam giác vuông AHC ta có:

AC² = AH² + HC² ⇒ AH² = AC² − HC² = 2² − 1² = 3 ⇒ AH = $\sqrt{3}$ ≈ 1,73 (cm).

Vậy chiều cao của tam giác đều khoảng 1,73 cm.

Do 1 + 1 = 2 và 2 + 4 = 6 < 20 nên các bộ ba trong a) , b) đều không thỏa mãn bất đẳng thức tam giác nên không thể là độ dài ba cạnh của một tam giác.

Vì 5² = 3² + 4² và ${\left(2\sqrt{2}\right)}^2=2^2+2^2$ nên các bộ ba trong c), d) là độ dài ba cạnh của tam giác vuông (theo định lí Pythagore đảo).

Các tam giác trong Hình 9.43 đều là các tam giác vuông nên ta áp dụng định lí Pythagore.

+) x² = 4² + 2² = 20. Suy ra x = $2\sqrt{5}$.

+) 5² = 4² + y² nên y² = 5² − 4² = 9. Suy ra y = 3.

+) z² = ${\left(\sqrt{5}\right)}^2+{\left(2\sqrt{5}\right)}^2$= 25. Suy ra z = 5.

+) t² = 1² + 2² = 5. Suy ra t = $\sqrt{5}$.

Vì tam giác ABC cân tại A có đường cao AH nên AH cũng là đường trung tuyến hay H là trung điểm BC. Suy ra HB = HC = BC : 2 = 10 : 2 = 5 cm.

Xét tam giác AHB vuông tại H, theo định lí Pythagore ta có

AB² = AH² + HB² = 3² + 5² = 34.

Suy ra AB = $\sqrt{34}$ cm.

Do tam giác ABC cân tại A nên AC = AB = $\sqrt{34}$ cm.

Áp dụng định lí Pythagore cho tam giác ABC vuông tại B ta có: AB² + BC² = AC².

Suy ra BC² = AC² – AB² = 17² – 8² = 225.

Do đó, BC = 15 (cm).

Diện tích của hình chữ nhật là: AB . BC = 8 . 15 = 120 (cm²).

- Áp dụng định lí Pythagore cho tam giác ABE vuông tại B, có 

 AE² = AB² + BE² = 5² + 3² = 34.

Suy ra AE = $\sqrt{34}$ m < 6 m.

Suy ra chú cún có thể chạy đến điểm E do khoảng cách AE ngắn hơn sợi dây.

- Áp dụng định lí Pythagore cho tam giác ADF vuông tại D, có 

 AF² = AD² + DF² = 5² + 4² = 41.

Suy ra AE = $\sqrt{41}$ m > 6 m.

Suy ra chú cún không thể chạy đến điểm F do khoảng cách AF dài hơn sợi dây.

- Áp dụng định lí Pythagore cho tam giác ADC vuông tại D, có 

 AC² = AD² + DC² = 5² + 5² = 50.

Suy ra AE = $5\sqrt{2}$ m > 6 m.

Suy ra chú cún không thể chạy đến điểm C do khoảng cách AC dài hơn sợi dây.

Vậy chú cún không thể chạy hết tất cả các điểm của mảnh vườn. Chú chó chỉ có thể chạy đến điểm B, D, E.