Câu hỏi:
27/07/2023 3,216
Sử dụng tính chất hai đường chéo của hình chữ nhật bằng nhau để chứng minh a), b) của ý 1.
Sử dụng tính chất hai đường chéo của hình chữ nhật bằng nhau để chứng minh a), b) của ý 1.
Câu hỏi trong đề: Giải SBT Toán 8 KNTT Bài 13: Hình chữ nhật có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
M là trung điểm của cạnh BC của tam giác ABC; lấy điểm P sao cho M là trung điểm của AP thì ABPC là một hình bình hành.
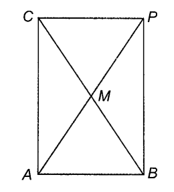
a) Nếu tam giác ABC vuông tại A thì hình bình hành ABPC có nên ABPC là hình chữ nhật.
Do đó hai đường chéo BC, AP bằng nhau, suy ra MA = MB = MC = MP.
b) Nếu có M thuộc BC sao cho thì suy ra BC = AP;
Khi đó hình bình hành ABPC có hai đường chéo bằng nhau nên là hình chữ nhật.
Vậy tam giác ABC vuông tại A.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
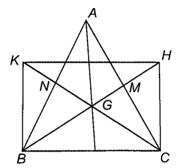
Vì BM, CN là trung tuyến của ∆ABC nên M, N lần lượt là trung điểm của AC, AB.
Do M là trung điểm của AC và của GH nên AGCH là hình bình hành
Từ đó HC = AG và HC // AG. (1)
Do N là trung điểm của AB và của GK nên AGBK là hình bình hành
Suy ra KB = AG và KB // AG. (2)
Từ (1) và (2) suy ra BK = CH và BK // CH.
Tứ giác BCHK có hai cạnh đối BK, CH bằng nhau và song song nên là một hình bình hành.
Vì tam giác ABC cân tại A nên trung tuyến AG là đường cao tức AG ⊥ BC hay KB ⊥ BC, suy ra BCHK là hình chữ nhật.
Lời giải
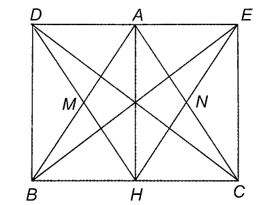
a) • Tứ giác AHBD có M là trung điểm của AB và HD nên là hình bình hành.
Do AH là đường cao của ∆ABC nên AH ⊥ BC, suy ra
Hình bình hành AHBD có nên AHBD là hình chữ nhật.
• Tương tự, tứ giác AHCE có N là trung điểm của AC và HE nên là hình bình hành.
Lại có nên AHCE là hình chữ nhật.
• Do AHBD, AHCE là các hình chữ nhật (chứng minh trên)
Suy ra
Tứ giác BCED có là các góc ở đỉnh nên BCED là hình chữ nhật.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 25
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
Đề cuối kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án- Đề 4
-
Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án (Đề 5)
-
Dạng 8: Bài luyện tập 3 dạng 4. Tổng hợp có đáp án