Câu hỏi:
29/07/2024 1,164
Nếu một hình chóp tứ chóp tứ giác đều có cạnh đáy bằng 2 và có diện tích xung quanh bằng \(4\sqrt 3 \) thì có thể tích bằng
Đáp án chính xác
Quảng cáo
Trả lời:
Giải bởi Vietjack
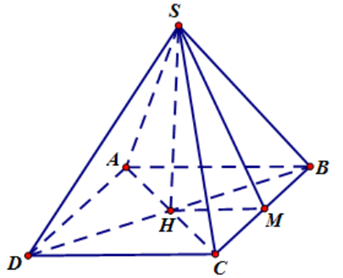
Xét hình chóp đều \[S.ABCD\] như hình vẽ.
Kẻ \(OM \bot BC \Rightarrow M\) là trung điểm \[BC\] và \(BC \bot (SOM).\)
Do đó \(BC \bot SM.\)
Xét \(\Delta SOM\) vuông tại \(O\), ta có:
\(S{M^2} = S{O^2} + O{M^2} \Rightarrow SM = \sqrt {S{O^2} + 1} .\)
Mặt khác, \({S_{xq}} = 4{S_{SBC}} \Leftrightarrow 4\sqrt 3 = 4 \cdot \frac{1}{2} \cdot SM \cdot BC\)
\( \Leftrightarrow 4\sqrt 3 = 2 \cdot \sqrt {S{O^2} + 1} \cdot 2 \Leftrightarrow SO = \sqrt 2 \,\,(x > 0).\)
\({V_{S.ABCD}} = \frac{1}{3} \cdot SO \cdot {S_{ABCD}} = \frac{1}{3} \cdot \sqrt 2 \cdot {2^2} = \frac{{4\sqrt 2 }}{3}\) (đvtt). Chọn A.
Nhà sách vietjack
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Biết rằng \(\frac{{\left( {2 - a} \right)x - 3}}{{\sqrt {{x^2} + 1} - x}}\) có giới hạn là \( + \infty \) khi \(x \to + \infty \) (với \(a\) là tham số). Tính giá trị nhỏ nhất của \(P = {a^2} - 2a + 4.\)
Đáp án: ……….
Biết rằng \(\frac{{\left( {2 - a} \right)x - 3}}{{\sqrt {{x^2} + 1} - x}}\) có giới hạn là \( + \infty \) khi \(x \to + \infty \) (với \(a\) là tham số). Tính giá trị nhỏ nhất của \(P = {a^2} - 2a + 4.\)
Đáp án: ……….
Xem đáp án »
29/07/2024
6,862
Câu 2:
Nội dung nào sau đây không phải là ý nghĩa quốc tế của cuộc kháng chiến chống thực dân Pháp xâm lược (1945-1954) của quân dân Việt Nam?
Xem đáp án »
29/07/2024
3,041
Câu 3:
Trong không gian \[Oxyz,\] cho điểm \(A\left( {2\,;\,\, - 1\,;\,\, - 3} \right)\) và mặt phẳng \(\left( P \right):3x - 2y + 4z - 5 = 0.\) Mặt phẳng \(\left( Q \right)\) đi qua \(A\) và song song với mặt phẳng \(\left( P \right)\) có phương trình là
Xem đáp án »
29/07/2024
2,733
Câu 4:
Diện tích hình phẳng giới hạn bởi các đường \((P):y = {x^2} - 2x + 2\), trục tung tiếp tuyến của \(\left( P \right)\) tại \(M\left( {3\,;\,\,5} \right)\) là
Đáp án: ……….
Diện tích hình phẳng giới hạn bởi các đường \((P):y = {x^2} - 2x + 2\), trục tung tiếp tuyến của \(\left( P \right)\) tại \(M\left( {3\,;\,\,5} \right)\) là
Đáp án: ……….
Xem đáp án »
29/07/2024
2,087
Câu 5:
Từ 5 chữ số \[0\,;\,\,1\,;\,\,3\,;\,\,5\,;\,\,7\] có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số đôi một khác nhau và không chia hết cho 5?
Đáp án: ……….
Từ 5 chữ số \[0\,;\,\,1\,;\,\,3\,;\,\,5\,;\,\,7\] có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số đôi một khác nhau và không chia hết cho 5?
Đáp án: ……….
Xem đáp án »
29/07/2024
1,682
Câu 6:
Cho hình chóp đều \[S.ABC\] có cạnh đáy bằng 1. Gọi \[M\] là trung điểm của \[SA.\] Biết thể tích của khối chóp đó bằng \(\frac{{\sqrt 3 }}{2}\), khoảng cách từ điểm \[M\] đến mặt phẳng \(\left( {ABC} \right)\) bằng
Đáp án: ……….
Cho hình chóp đều \[S.ABC\] có cạnh đáy bằng 1. Gọi \[M\] là trung điểm của \[SA.\] Biết thể tích của khối chóp đó bằng \(\frac{{\sqrt 3 }}{2}\), khoảng cách từ điểm \[M\] đến mặt phẳng \(\left( {ABC} \right)\) bằng
Đáp án: ……….
Xem đáp án »
29/07/2024
1,621
Câu 7:
Ông An quyết định bán một phần mảnh đất hình chữ nhật có chu vi \[50{\rm{ }}m.\] Mảnh đất còn lại sau khi bán là một hình vuông cạnh bằng chiều rộng của mảnh đất hình chữ nhật ban đầu. biết giá tiền đất khi bán là \[1\,\,500\,\,000\] đồng.Hỏi số tiền lớn nhất mà ông An nhận được khi bán đất là bao nhiêu? (đơn vị: đồng).
Đáp án: ……….
Ông An quyết định bán một phần mảnh đất hình chữ nhật có chu vi \[50{\rm{ }}m.\] Mảnh đất còn lại sau khi bán là một hình vuông cạnh bằng chiều rộng của mảnh đất hình chữ nhật ban đầu. biết giá tiền đất khi bán là \[1\,\,500\,\,000\] đồng.Hỏi số tiền lớn nhất mà ông An nhận được khi bán đất là bao nhiêu? (đơn vị: đồng).
Đáp án: ……….
Xem đáp án »
29/07/2024
1,570
🔥 Đề thi HOT:
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 2)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 13)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận