Cho 5,2 gam hỗn hợp X (gồm ${\rm{Na}},{\rm{N}}{{\rm{a}}_2}{\rm{O}},{\rm{Ba}}$ và ${\rm{BaO}}$) vào ${{\rm{H}}_2}{\rm{O}}$ dư, thu được dung dịch ${\rm{Y}}$ và 0,02 mol ${{\rm{H}}_2}.$ Sục từ từ đến hết 0,07 mol ${\rm{C}}{{\rm{O}}_2}$ vào ${\rm{Y}}$, thu được dung dịch ${\rm{Z}}$ và ${\rm{m}}$ gam kết tủa ${\rm{BaC}}{{\rm{O}}_3}.$ Sự phụ thuộc của số mol kết tủa ${\rm{BaC}}{{\rm{O}}_3}({\rm{a}}\,{\rm{mol)}}$vào số mol ${\rm{C}}{{\rm{O}}_2}$ (b mol) được biểu diễn theo đồ thị bên dưới. Giá trị của m là

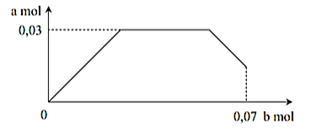
$Cho 5,2 gam hỗn hợp X (gồm dư, thu được dung dịch ${\rm{Y}}$ và 0,02 mol ${{\rm{H}}_2}.$ Sục từ từ đến hết 0,07 mol (ảnh 1)$

A. 1,97.

В. 3,94.

C. 5,91.

D. 7,88.

Xem lời giải

Câu hỏi trong đề: Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 21) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Tại thời điểm kết tủa lớn nhất ta có phản ứng: ${\rm{C}}{{\rm{O}}_2} + {\rm{Ba}}{({\rm{OH}})_2} \to {\rm{BaC}}{{\rm{O}}_3} + {{\rm{H}}_2}{\rm{O}}$

${n_{Ba\,\,(X)}} = {n_{{\rm{Ba}}{{({\rm{OH}})}_2}}} = 0,03\;{\rm{mol}} = {n_{{\rm{C}}{{\rm{O}}_2}}}$

Coi hỗn hợp ban đầu gồm có $\left\{ \begin{array}{l}Ba:0,03\,mol\\Na:x\,mol\\O:y\,mol\end{array} \right.$ ta có:

\[\left\{ {\begin{array}{*{20}{l}}{0,03.137 + 23x + 16y = 5,2}\\{2.0,03 + x = 2y + 0,02.2\,\,(BT\,\,electron)}\end{array} \Rightarrow \left\{ \begin{array}{l}x = 0,03\\y = 0,025\end{array} \right.(mol)} \right.\]

Khi số mol ${\rm{C}}{{\rm{O}}_2}$ bằng 0,07 mol, trong dung dịch tồn tại đồng thời gốc acid là ${\rm{HCO}}_3^ - $và ${\rm{CO}}_3^{2 - }$

$\sum {{n_{O{H^ - }\,\,(Y)}}} = 2{n_{B{a^{2 + }}}} + {n_{N{a^ + }}} = 2 \cdot 0,03 + 0,03 = 0,09\,mol$

Áp dụng công thức ta có:

${n_{{\rm{O}}{{\rm{H}}^ - }}} - {n_{{\rm{C}}{{\rm{O}}_2}}} = {n_{{\rm{CO}}_3^{2 - }}} \Rightarrow {n_{CO_3^{2 - }}} = 0,09 - 0,07 = 0,02\,\,mol$< 0,03 (${n_{B{a^{2 + }}}}$)

Þ Toàn bộ 0,02 mol $CO_3^{2 - }$đã kết hợp với $B{a^{2 + }}$để tạo kết tủa.

Vậy m = $0,02 \cdot 197 = 3,94$ gam.

Chọn B.

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Biết rằng $\frac{{\left( {2 - a} \right)x - 3}}{{\sqrt {{x^2} + 1} - x}}$ có giới hạn là $ + \infty $ khi $x \to + \infty $ (với $a$ là tham số). Tính giá trị nhỏ nhất của $P = {a^2} - 2a + 4.$

Đáp án: ……….

Xem đáp án

Lời giải

Ta có $\mathop {\lim }\limits_{x \to + \infty } \frac{{\left( {2 - a} \right)x - 3}}{{\sqrt {{x^2} + 1} - x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\left[ {\left( {2 - a} \right)x - 3} \right] \cdot \left( {\sqrt {{x^2} + 1} + x} \right)}}{{\left( {\sqrt {{x^2} + 1} - x} \right) \cdot \left( {\sqrt {{x^2} + 1} + x} \right)}}$

$ = \mathop {\lim }\limits_{x \to + \infty } \frac{{\left[ {\left( {2 - a} \right)x - 3} \right] \cdot \left( {\sqrt {{x^2} + 1} + x} \right)}}{{{x^2} + 1 - {x^2}}} = \mathop {\lim }\limits_{x \to + \infty } \left[ {\left( {2 - a} \right)x - 3} \right] \cdot \left( {\sqrt {{x^2} + 1} + x} \right)$

$ = \mathop {\lim }\limits_{x \to + \infty } {x^2}\left( {2 - a - \frac{3}{x}} \right) \cdot \left( {\sqrt {1 + \frac{1}{{{x^2}}}} + 1} \right)$

Vì $\mathop {\lim }\limits_{x \to + \infty } {x^2} = + \infty $ và $\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {1 + \frac{1}{{{x^2}}}} + 1} \right) = 2 > 0$ nên để $\mathop {\lim }\limits_{x \to + \infty } \frac{{\left( {2 - a} \right)x - 3}}{{\sqrt {{x^2} + 1} - x}} = + \infty $ thì

$\mathop {\lim }\limits_{x \to + \infty } {\left( {2 - a - \frac{3}{x}} \right)^ = } = 2 - a > 0 \Leftrightarrow a < 2.{\rm{ }}$

Khi đó $P = {a^2} - 2a + 4 = {\left( {a - 1} \right)^2} + 3 \ge 3$, vậy ${P_{\min }} = 3.$

Đáp án: 3.

Câu 2

Nội dung nào sau đây không phải là ý nghĩa quốc tế của cuộc kháng chiến chống thực dân Pháp xâm lược (1945-1954) của quân dân Việt Nam?

A. Giáng đòn nặng nề vào âm mưu nô dịch của chủ nghĩa đế quốc.

B. Mở đầu cho quá trình sụp đổ của chủ nghĩa thực dân kiểu mới.

C. Cổ vũ mạnh mē các dân tộc thuộc địa cùng đứng lên đấu tranh.

D. Góp phần thu hẹp hệ thống thuộc địa của chủ nghĩa thực dân.

Lời giải

Thắng lợi của cuộc kháng chiến chống thực dân Pháp xâm lược (1945-1954) của quân dân Việt Nam không mở đầu cho quá trình sụp đổ của chủ nghĩa thực dân kiểu mới trên thế giới vì thực dân Pháp là thực dân kiểu cũ. Chọn B.

Câu 3

Trong không gian \[Oxyz,\] cho điểm $A\left( {2\,;\,\, - 1\,;\,\, - 3} \right)$ và mặt phẳng $\left( P \right):3x - 2y + 4z - 5 = 0.$ Mặt phẳng $\left( Q \right)$ đi qua $A$ và song song với mặt phẳng $\left( P \right)$ có phương trình là

A. $\left( Q \right):3x - 2y + 4z - 4 = 0.$

B. $\left( Q \right):3x - 2y + 4z + 4 = 0.$

C. $\left( Q \right):3x - 2y + 4z + 5 = 0.$

D. $\left( Q \right):3x + 2y + 4z + 8 = 0.$

Lời giải