Trong thí nghiệm khe Y–âng ta thu được hệ thống vân sáng, vân tối trên màn. Xét hai điểm A, B đối xứng qua vân trung tâm, khi màn cách mặt phẳng chứa hai khe một khoảng là D thì A, B là vân sáng. Dịch chuyển màn ra xa hai khe một khoảng d thì A, B là vân sáng và đếm được số vân sáng trên đoạn AB trước và sau dịch chuyển màn hơn kém nhau 4. Nếu dịch tiếp màn ra xa hai khe một khoảng 9d nữa thì A, B là vân sáng và nếu dịch tiếp màn ra xa nữa thì tại A và B không còn xuất hiện vân sáng nữa. Tại A khi chưa dịch chuyển màn là vân sáng thứ mấy?
Trong thí nghiệm khe Y–âng ta thu được hệ thống vân sáng, vân tối trên màn. Xét hai điểm A, B đối xứng qua vân trung tâm, khi màn cách mặt phẳng chứa hai khe một khoảng là D thì A, B là vân sáng. Dịch chuyển màn ra xa hai khe một khoảng d thì A, B là vân sáng và đếm được số vân sáng trên đoạn AB trước và sau dịch chuyển màn hơn kém nhau 4. Nếu dịch tiếp màn ra xa hai khe một khoảng 9d nữa thì A, B là vân sáng và nếu dịch tiếp màn ra xa nữa thì tại A và B không còn xuất hiện vân sáng nữa. Tại A khi chưa dịch chuyển màn là vân sáng thứ mấy?
Quảng cáo
Trả lời:
Giả sử ban đầu A là vị trí cho vân sáng bậc \(k \to {x_M} = k\frac{{D{\rm{\lambda }}}}{a}\) (1)
Khi dịch chuyển màn ra xa một đọan d thì A vẫn là vân sáng nhưng số vân sáng trên AB giảm đi 4 vân điều này chứng tỏ tại A lúc này là vân sáng bậc \(\left( {{\rm{k}} - 2} \right)\)\( \to {{\rm{x}}_{\rm{M}}} = ({\rm{k}} - 2)\frac{{({\rm{D}} + {\rm{d}}){\rm{\lambda }}}}{{\rm{a}}}\)
Từ (1) và (2): \(k\frac{{D{\rm{\lambda }}}}{a} = ({\rm{k}} - 2)\frac{{({\rm{D}} + {\rm{d}}){\rm{\lambda }}}}{{\rm{a}}} \Rightarrow \)\({\rm{k}} = ({\rm{k}} - 2)\left( {1 + \frac{{\rm{d}}}{{\rm{D}}}} \right)\)(*)
Tiếp tục dịch chuyển màn ra xa thêm một khoảng 9d nữa thì A là vân sáng, sau đó nếu dịch chuyển màn tiếp tục ra xa thì ta sẽ không thu được vân sáng nên lúc này A là vân sáng bậc nhất
\( \Rightarrow {{\rm{x}}_{\rm{M}}} = \frac{{({\rm{D}} + 10\;{\rm{d}}){\rm{\lambda }}}}{{\rm{a}}}\) (3)
Từ (1) và (3): \(k\frac{{D{\rm{\lambda }}}}{a} = \frac{{({\rm{D}} + 10\;{\rm{d}}){\rm{\lambda }}}}{{\rm{a}}} \Rightarrow {\rm{kD}} = {\rm{D}} + 10\;{\rm{d}} \Rightarrow \frac{{\rm{d}}}{{\rm{D}}} = \frac{{{\rm{k}} - 1}}{{10}}\)
Thay vào phương trình (*) ta thu được \(\frac{{{{\rm{k}}^2}}}{{10}} - \frac{3}{{10}}{\rm{k}} - \frac{9}{5} = 0 \to {\rm{k}} = 6\). Chọn D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
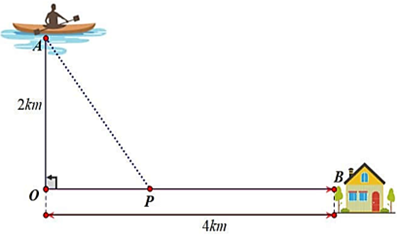
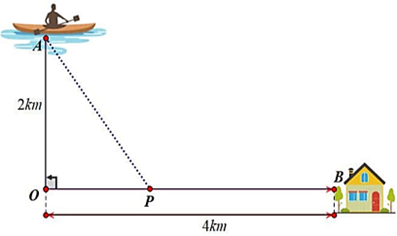
Đặt \(OP = x\,\,(0 < x < 4) \Rightarrow BP = 4 - x\,;\,\,AP = \sqrt {4 + {x^2}} .\)
Khoảng thời gian để anh Ba từ vị trí xuất phát đến được điểm \(B\) là:
\({t_{\left( x \right)}} = {t_{AP}} + {t_{PB}} = \frac{{\sqrt {4 + {x^2}} }}{6} + \frac{{4 - x}}{{10}}(h)\,\, \Rightarrow {t'_{\left( x \right)}} = \frac{x}{{6\sqrt {4 + {x^2}} }} - \frac{1}{{10}}.\)
\({t'_{\left( x \right)}} = 0 \Leftrightarrow \frac{x}{{6\sqrt {4 + {x^2}} }} - \frac{1}{{10}} = 0 \Leftrightarrow 3\sqrt {4 + {x^2}} = 5x \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{0 < x < 4}\\{4{x^2} = 9}\end{array} \Leftrightarrow x = \frac{3}{2}.} \right.\)
Bảng biến thiên:
|
\(x\) |
0 |
\(\frac{3}{2}\) |
4 |
|
\(t'\left( x \right)\) |
\( - \) |
0 + |
|
|
\(t\left( x \right)\) |
\(\frac{{11}}{{15}}\)
|
|
\(\frac{{\sqrt 5 }}{3}\)
|
|
|
|
\(\frac{2}{3}\) |
|
Từ bảng biến thiên suy ra khoảng thời gian ngắn nhất để anh Ba từ vị trí xuất phát đến được điểm \({\rm{B}}\) là: \({t_{\min }} = \frac{2}{3}(h) = \frac{2}{3}.60\) (phút) \( = 40\) (phút). Chọn A.
Lời giải
Gọi vị trí thấp nhất của ống bương là là vị trí của máng nước (như hình vẽ).
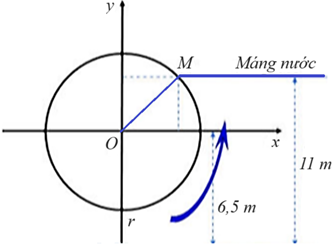
Tung độ của điểm \[M\] là \({y_M} = 11 - 6,5 = 4,5\)
\( \Rightarrow \sin \widehat {xOM} = \frac{{{y_M}}}{{OM}} = \frac{{4,5}}{5} = 0,9 \Rightarrow \widehat {xOM} \approx 64^\circ \).
Ta có \(\widehat {TOM} = \widehat {TOx} + \widehat {xOM} = 90^\circ + 64^\circ = 154^\circ .\)
Vì thời gian cọn nước thực hiện 1 vòng quay là 3 phút nên thời gian ống bương di chuyển từ \(T\)đến \(M\) là \(\frac{{3.154}}{{360}} = \frac{{77}}{{60}}\) (phút). Chọn C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(x = 2.\)
B. \(x = 3.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.