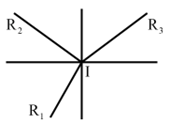
Trong một thí nghiệm về sự khúc xạ ánh sáng, một học sinh ghi lại trên tấm bìa ba đường truyền của ánh sáng như hình vẽ, nhưng quên ghi chiều truyền. (Các) tia nào kể sau có thể là tia khúc xạ?

Quảng cáo
Trả lời:
Theo định luật khúc xạ ánh sáng: Tia khúc xạ nằm trong mặt phẳng tới và nằm phía bên kia pháp tuyến so với tia tới.
Tia IR1 là tia khúc xạ, tia IR2 là tia phản xạ, tia IR3 là tia tới. Chọn A.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x\) (nghìn đồng) là giá phòng khách sạn sau khi tăng giá \((x > 400).\)
Giá chênh lệch sau khi tăng là: \(x - 400\) (nghìn đồng).
Số phòng trống lúc này là: \(2 \cdot \frac{{x - 400}}{{20}} = \frac{{x - 400}}{{10}}\) (phòng).
Số phòng cho thuê lúc này là: \(50 - \frac{{x - 400}}{{10}} = \frac{{900 - x}}{{10}}\) (phòng).
Số tiền phòng thu được là: \(f\left( x \right) = x \cdot \left( {\frac{{900 - x}}{{10}}} \right) = \frac{{ - {x^2} + 900x}}{{10}}\) (nghìn đồng).
Ta cần tìm \(x > 400\) sao cho \(f\left( x \right)\) đạt giá trị lớn nhất.
Dễ thấy \(x = - \frac{{900}}{{2 \cdot ( - 1)}} = 450\) thì lớn nhất. Đáp án: 450.
Câu 2
A. \(T = 6.\)
B. \(T = 0.\)
Lời giải
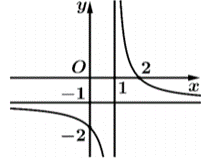
Từ đồ thị ta có:
• TCĐ: \(x = 1 \Rightarrow \frac{{ - d}}{{{c_a}}} = 1 \Rightarrow \frac{d}{c} = - 1 \Rightarrow d = - c\);
• TCN: \(y = - 1 \Rightarrow \frac{a}{c} = - 1 \Rightarrow a = - c\).
Đồ thị cắt trục hoành tại điểm: \(x = 2 \Rightarrow \frac{{ - b}}{a} = 2 \Rightarrow \frac{{ - b}}{{ - c}} = 2 \Rightarrow b = 2c\)
Vậy \(T = \frac{{a - 2b + 3d}}{c} = \frac{{ - c - 4c - 3c}}{c} = - 8\). Chọn C.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(4x - 3y + 18 = 0.\)
B. \(4x - 3y - 18 = 0.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.