Một loài thực vật, xét 2 cặp gen phân li độc lập, alen A quy định thân cao trội hoàn toàn so với alen a quy định thân thấp, alen B quy định khả năng chịu mặn trội hoàn toàn so với alen b quy định không có khả năng chịu mặn; cây có kiểu gen bb không có khả năng sống khi trồng trong đất ngập mặn và hạt có kiểu gen bb không nảy mầm trong đất ngập mặn. Để nghiên cứu và ứng dụng trồng rừng phòng hộ ven biển, người ta cho 2 cây (P) dị hợp 2 cặp gen giao phấn với nhau để tạo ra các cây F1 ở vườn ươm không nhiễm mặn; sau đó chọn tất cả các cây thân cao F1 đem trồng ở vùng đất ngập mặn ven biển. Các cây này giao phấn ngẫu nhiên tạo ra F2. Theo thuyết, trong tổng số cây F2 ở vùng đất này, số cây thân cao, chịu mặn chiếm tỉ lệ bao nhiêu?
Đáp án: ……….
Một loài thực vật, xét 2 cặp gen phân li độc lập, alen A quy định thân cao trội hoàn toàn so với alen a quy định thân thấp, alen B quy định khả năng chịu mặn trội hoàn toàn so với alen b quy định không có khả năng chịu mặn; cây có kiểu gen bb không có khả năng sống khi trồng trong đất ngập mặn và hạt có kiểu gen bb không nảy mầm trong đất ngập mặn. Để nghiên cứu và ứng dụng trồng rừng phòng hộ ven biển, người ta cho 2 cây (P) dị hợp 2 cặp gen giao phấn với nhau để tạo ra các cây F1 ở vườn ươm không nhiễm mặn; sau đó chọn tất cả các cây thân cao F1 đem trồng ở vùng đất ngập mặn ven biển. Các cây này giao phấn ngẫu nhiên tạo ra F2. Theo thuyết, trong tổng số cây F2 ở vùng đất này, số cây thân cao, chịu mặn chiếm tỉ lệ bao nhiêu?
Đáp án: ……….
Quảng cáo
Trả lời:
Ta có: \({\rm{P}}:{\rm{AaBb}} \times {\rm{AaBb}} \to {{\rm{F}}_1}:(1{\rm{AA}}:2{\rm{Aa}}:1{\rm{aa}}) \times (1{\rm{BB}}:2{\rm{Bb}}:1{\rm{bb}})\).
Chọn các cây thân cao A- đem trồng ở đất ngập mặn (chỉ có các cây B- là sống được) thì tỉ lệ kiểu gen các cây sống được là: (1AA : 2Aa)×(1BB : 2Bb).
Cho các cây F1 sống được giao phấn ngẫu nhiên: (2A : 1a)×(2B : 1b)
→ Tỉ lệ kiểu gen các hạt \({{\rm{F}}_2}\) thu được là: (4AA : 4Aa : 1aa)(4BB : 4Bb : 1bb).
→ Tỉ lệ kiểu gen các cây \({{\rm{F}}_2}\) sống được ở vùng đất mặn này là: (4AA : 4Aa : 1aa)(1BB : 1Bb).
→ Trong số cây \({{\rm{F}}_2}\) sống ở vùng đất này thì cây thân cao chịu mặn A-B- chiếm tỉ lệ là \(\frac{8}{9}.\)
Đáp án: \(\frac{8}{9}.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
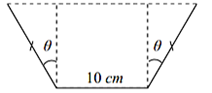
Gọi chiều cao máng nước là: \(h = 10 \cdot \cos \theta \,\,({\rm{cm}})\).
Chiều dài đáy trên máng nước là:
\(10 + 2 \cdot \sqrt {{{10}^2} - {h^2}} = 10 + 2 \cdot \sqrt {{{10}^2} - {{\left( {10 \cdot \cos \theta } \right)}^2}} = 10 + 20 \cdot \sin \theta \,\,({\rm{cm}})\).
Máng nước chứa được nhiều nước nhất khi diện tích hình vẽ lớn nhất
\( \Leftrightarrow S = \frac{{10 + 20 \cdot \sin \theta + 10}}{2} \cdot 10 \cdot \cos \theta = 100 \cdot (1 + \sin \theta ) \cdot \cos \theta = 100 \cdot \left( {\cos \theta + \frac{{\sin 2\theta }}{2}} \right)\).
Ta có \(S' = 100\left( { - \sin \theta + \cos 2\theta } \right) = 100\left( { - \sin \theta + 1 - 2{{\sin }^2}\theta } \right)\)
Khi đó \(S' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\sin \theta = - 1}\\{\sin \theta = \frac{1}{2}}\end{array}} \right.\).
Ta có bảng biến thiên:
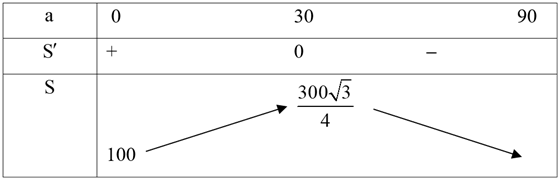
Do đó \({S_{\max }} \Leftrightarrow \sin \theta = \frac{1}{2} \Leftrightarrow \sin \theta = 30^\circ {\rm{.}}\) Đáp án: 30.
Lời giải
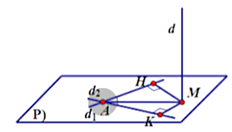
Ta có: \(\overrightarrow {{n_P}} = \left( {1\,;\,\,0\,;\,\, - 1} \right),\,\,\overrightarrow {{u_d}} = \left( { - 1\,;\,\,0\,;\,\,1} \right)\)
\( \Rightarrow d \bot \left( P \right)\) và \(d \cap (P) = M\left( {0\,;\,\,2\,;\,\, - 1} \right)\)
\( \Rightarrow \overrightarrow {MA} = (2; - 1;2) \Rightarrow MA = 3\)
Gọi \[H,\,\,K\] lần lượt là hình chiếu vuông góc của \(M\) lên \({d_1}\) và \({d_2},\) ta có\(d\left( {{d_1}\,;\,\,d} \right) = d\left( {M\,;\,\,{d_1}} \right) = MH,\,\,\,d\left( {{d_2}\,;\,\,d} \right) = d\left( {M\,;\,\,{d_2}} \right) = MK\)
\( \Rightarrow MH = MK = \sqrt 6 \) \( \Rightarrow \sin \widehat {MAK} = \sin \widehat {MAH} = \frac{{HM}}{{AM}} = \frac{{\sqrt 6 }}{3}\)
\( \Rightarrow \cos \left( {{d_1};\,\,{d_2}} \right) = \left| {\cos \left( {2 \cdot \widehat {MAH}} \right)} \right| = \left| {1 - 2{{\sin }^2}\widehat {MAH}} \right| = \left| {1 - \frac{4}{3}} \right| = \frac{1}{3}.\) Đáp án: \(\frac{1}{3}.\)
Câu 3
A. \(S = 4,8.\)
B. \(S = 3,9.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.