Câu hỏi:
25/08/2024 1,461
Khi quay tam giác OHA vuông cân ở H một vòng xung quanh đường thẳng cố định OH, ta được một hình nón như ở Hình 14. Hỏi diện tích xung quanh của hình nón đó là bao nhiêu centimét vuông (làm tròn kết quả đến hàng đơn vị)? Biết diện tích tam giác OHA là 4 cm2.
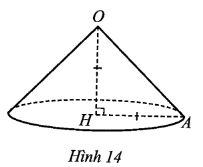
Khi quay tam giác OHA vuông cân ở H một vòng xung quanh đường thẳng cố định OH, ta được một hình nón như ở Hình 14. Hỏi diện tích xung quanh của hình nón đó là bao nhiêu centimét vuông (làm tròn kết quả đến hàng đơn vị)? Biết diện tích tam giác OHA là 4 cm2.
Câu hỏi trong đề: Giải SBT Toán 9 Bài 2. Hình nón có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có diện tích của tam giác OHA vuông tại H là \[\frac{1}{2}OH \cdot HA\] (cm2).
Theo bài, tam giác OHA vuông cân tại H có diện tích bằng 4 cm2 nên \[\frac{1}{2}OH \cdot HA = 4\]
Suy ra OH.HA = 8
Do đó \[OH = HA = 2\sqrt 2 \] cm (do ∆OHA vuông cân tại H).
Xét ∆OHA vuông tại H, theo định lí Pythagore, ta có:
OA2 = OH2 + HA2
Suy ra \[OA = \sqrt {{{\left( {2\sqrt 2 } \right)}^2} + {{\left( {2\sqrt 2 } \right)}^2}} = \sqrt {8 + 8} = \sqrt {16} = 4\] (cm).
Vậy diện tích xung quanh của hình nón đó là:
\(\pi \cdot HA \cdot OA = \pi \cdot 2\sqrt 2 \cdot 4 = 8\sqrt 2 \pi \approx 8\sqrt 2 \cdot 3,14 \approx 36\;\) (cm2).
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi bán kính đường tròn đáy của đống cát hình nón đó là r (m) (r > 0).
Do hình nón có chu vi đáy bằng 9,42 m nên ta có 2πr = 9,42 (m).
Suy ra: \(r = \frac{{9,42}}{{2\pi }} \approx \frac{{9,42}}{{2 \cdot 3,14}} = 1,5\;\) (m).
Thể tích đống cát có dạng hình nón là:
\(\frac{1}{3}\pi {r^2}h \approx \frac{1}{3} \cdot 3,14 \cdot 1,{5^2} \cdot 1,2 = 2,826\;\) (m3).
Thể tích thùng chứa của xe có dạng hình hộp chữ nhật là:
1,57 . 0,8 . 0,4 = 0,5024 (m3).
Mỗi chuyến xe thực chở là:
0,5024.(100% – 5%) = 0,5024 . 95% = 0,47728 (m3).
Ta có: 2,826 : 0,47728 ≈ 5,921.
Vậy để chuyển hết đống cát trên bác Hà cần sử dụng ít nhất 6 chuyến xe và phải dùng số tiền ít nhất là: 6 . 90 000 = 540 000 (đồng).
Lời giải
Lượng kem ở phía trong cốc của một chiếc kem chính là thể tích của hình nón có bán kính là \(\frac{6}{2} = 3\) cm và chiều cao là 10 cm, và bằng:
\[\frac{1}{3} \cdot \pi \cdot {3^2} \cdot 10 = 30\pi \;({\rm{c}}{{\rm{m}}^3}).\]
Lượng kem đổ dư thêm lên phía trên miệng cốc của một chiếc kem là:
30π. 10% = 3π (cm3).
Lượng kem mà cơ sở sản xuất A cần chuẩn bị để làm ra 1 500 chiếc kem là:
(30π + 3π) .1 500 = 49 500π ≈ 49 500 . 3,14 = 155 430 (cm3).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo