Câu hỏi:
28/08/2024 14,733
Cho tam giác nhọn ABC (AB < AC) có hai đường cao BD và CE.
a) Chứng minh bốn điểm B, C, D, E cùng thuộc một đường tròn.
b) Vẽ đường tròn (B; BD). Chứng minh AC là tiếp tuyến của đường tròn (B; BD).
c) Đường tròn (B; BD) cắt CE tại K(K nằm giữa E và C). Qua D vẽ đường thẳng vuông góc với BC tại H và cắt đường thẳng AB tại M. Chứng minh \(\widehat {BMH} = \widehat {BKH}.\)
Cho tam giác nhọn ABC (AB < AC) có hai đường cao BD và CE.
a) Chứng minh bốn điểm B, C, D, E cùng thuộc một đường tròn.
b) Vẽ đường tròn (B; BD). Chứng minh AC là tiếp tuyến của đường tròn (B; BD).
c) Đường tròn (B; BD) cắt CE tại K(K nằm giữa E và C). Qua D vẽ đường thẳng vuông góc với BC tại H và cắt đường thẳng AB tại M. Chứng minh \(\widehat {BMH} = \widehat {BKH}.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
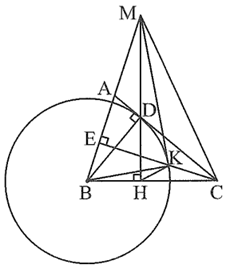
a) Ta có BD ⊥ AC, CE ⊥ AB nên tam giác BEC vuông tại E và tam giác BDC vuông tại D.
∆BEC vuông tại E nên nội tiếp đường tròn đường kính BC. (1)
∆BDC vuông tại D nên nội tiếp đường tròn đường kính BC. (2)
Từ (1) và (2) suy ra bốn điểm B, C, D, E cùng thuộc đường tròn đường kính BC.
b) Ta có BD là bán kính đường tròn (B; BD) và BD ⊥ AC nên AC là tiếp tuyến của đường tròn (B; BD).
c) Xét ∆BHD và ∆BDC có:
Góc B chung; \[\widehat {BHD} = \widehat {BDC} = 90^\circ \]
Do đó ∆BHD ᔕ ∆BDC (g.g)
Suy ra \[\frac{{BD}}{{BC}} = \frac{{BH}}{{BD}}\] hay BD2 = BH.BC.
Ta lại có BD = BK (bán kính đường tròn (B; BD)) nên BK2 = BH.BC.
Suy ra \[\frac{{BH}}{{BK}} = \frac{{BK}}{{BC}}\]
Xét ∆BHK và ∆BKC có:
Góc B chung; \[\frac{{BH}}{{BK}} = \frac{{BK}}{{BC}}\]
Do đó ∆BHK ᔕ ∆BKC (c.g.c)
Suy ra \(\widehat {BKH} = \widehat {BCK}\) (hai góc tương ứng).
Mà \(\widehat {BMH} = \widehat {BCK}\) (cùng phụ với \(\widehat {ABC})\) nên \(\widehat {BMH} = \widehat {BKH}.\)
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
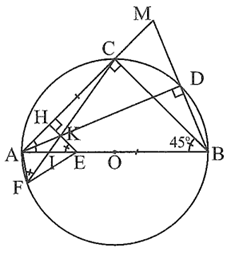
a) Ta có \(\widehat {ACB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn (O) đường kính AB), suy ra BC ⊥ AC.
Mà EH ⊥ AC (giả thiết), suy ra EH // BC.
b) Vì C là điểm chính giữa của cung AB và AB là đường kính của đường tròn (O), suy ra
Vì AD là tia phân giác của \(\widehat {BAC}\) (giả thiết) nên \(\widehat {CAD} = \widehat {BAD} = \frac{1}{2}\widehat {CAB},\) suy ra
Xét đường tròn (O) có:
⦁ \(\widehat {CAB}\) là góc nội tiếp chắn cung CB nên
⦁ \(\widehat {CBA}\) là góc nội tiếp chắn cung CA nên
⦁ \(\widehat {CBD}\) là góc nội tiếp chắn cung CD nên
Suy ra \(\widehat {MAB} = 45^\circ ;\) \(\widehat {MBA} = \widehat {MBC} + \widehat {CBA} = 22,5^\circ + 45^\circ = 67,5^\circ .\)
Xét ∆MAB có: \[\widehat {AMB} + \widehat {MAB} + \widehat {MBA} = 180^\circ \]
Suy ra \[\widehat {AMB} = 180^\circ - \widehat {MAB} - \widehat {MBA} = 180^\circ - 45^\circ - 67,5^\circ = 67,5^\circ .\]
c) Vì EH // BC nên \(\widehat {AEK} = \widehat {ABC}\) (hai góc đồng vị).
Mà \(\widehat {AFK} = \widehat {AFC} = \widehat {ABC}\) (góc nội tiếp cùng chắn cung AC của đường tròn (O)).
Suy ra \(\widehat {AEK} = \widehat {AFK}.\)
d) Tam giác AIC có AK là tia phân giác của \(\widehat {CAI},\) suy ra \(\frac{{AI}}{{AC}} = \frac{{KI}}{{KC}}.\)
Tam giác CIB có EK // CB, suy ra \(\frac{{IE}}{{BE}} = \frac{{KI}}{{KC}}\) (định lí Thalès)
Từ (1) và (2) suy ra \(\frac{{AI}}{{AC}} = \frac{{IE}}{{BE}}.\)
Mà AC = BE (giả thiết) nên AI = IE.
Vậy I là trung điểm của đoạn thẳng AE.
Lời giải
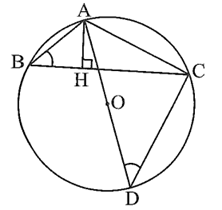
a) Ta có: \(\widehat {ACD}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {ACD} = 90^\circ .\)
Xét đường tròn (O) có \(\widehat {ABC} = \widehat {ADC}\) (hai góc nội tiếp cùng chắn cung AC) hay \(\widehat {ABH} = \widehat {ADC}.\)
Xét ∆AHB và ∆ACD có:
\(\widehat {AHB} = \widehat {ACD} = 90^\circ ;\) \(\widehat {ABH} = \widehat {ADC}\)
Do đó ∆AHB ᔕ ∆ACD (g.g).
b) Vì ∆AHB ᔕ ∆ACD (câu a) nên \(\frac{{AH}}{{AC}} = \frac{{AB}}{{AD}}\)
Hay AH.AD = AB.AC, suy ra \(AD = \frac{{AB \cdot AC}}{{AH}} = \frac{{8 \cdot 15}}{5} = 24\) (cm).
Do đó độ dài bán kính của đường tròn (O) là \(\frac{{AD}}{2} = \frac{{24}}{2} = 12\) cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
-
Đề ôn thi vào 10 môn Toán có đáp án (Mới nhất)- Đề số 1