Giải SBT Toán 9 Chân trời sáng tạo Bài tập cuối chương 9 quay có đáp án
34 người thi tuần này 4.6 364 lượt thi 17 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án
Danh sách câu hỏi:
Lời giải
Đáp án đúng là: D
Do ∆ABC vuông có hai cạnh góc vuông là 5 cm, 12 cm nên áp dụng định lí Pythagore, ta có độ dài cạnh huyền bằng: \[\sqrt {{5^2} + {{12}^2}} = \sqrt {169} = 13\] (cm).
Bán kính của đường tròn ngoại tiếp tam giác ABC có độ dài là \[\frac{{13}}{2} = 6,5\] (cm).
Lời giải
Đáp án đúng là: A
Bán kính đường tròn nội tiếp tam giác đều cạnh \(8a\sqrt 3 \) là \[\frac{{8a\sqrt 3 \cdot \sqrt 3 }}{6} = \frac{{24a}}{6} = 4a.\]
Lời giải
Đáp án đúng là: B
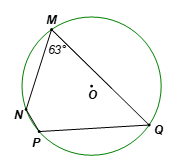
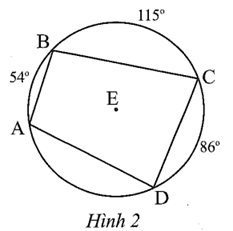
Do tứ giác MNPQ nội tiếp đường tròn (O; R) nên tổng hai góc đối bằng 180°
Suy ra \[\widehat M + \widehat P = 180^\circ \]
Do đó \[\widehat P = 180^\circ - \widehat M = 180^\circ - 63^\circ = 117^\circ .\]
Lời giải
Đáp án đúng là: C
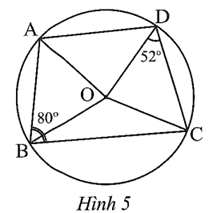
Tam giác ABD có \[\widehat A = 90^\circ \] nên ∆ABD vuông tại A, do đó AD là đường kính của đường tròn ngoại tiếp ∆ABD hay chính là đường tròn (O; R).
Suy ra bán kính của đường tròn (O; R) là \[R = \frac{1}{2}BD = \frac{1}{2} \cdot 12 = 6\] (cm).
Vậy độ dài của bán kính R của đường tròn (O; R) là 6 cm.
Lời giải
Đáp án đúng là: A
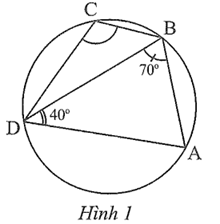
Xét ∆ABD có \(\widehat {BAD} + \widehat {ABD} + \widehat {DAB} = 180^\circ \)
Suy ra \(\widehat {BAD} = 180^\circ - \widehat {ABD} - \widehat {DAB} = 180^\circ - 70^\circ - 40^\circ = 70^\circ .\)
Do tứ giác ABCD nội tiếp đường tròn nên hai góc đối nhau của tứ giác bằng 180°, hay \(\widehat {BAD} + \widehat {BCD} = 180^\circ \)
Suy ra \(\widehat {BCD} = 180^\circ - \widehat {BAD} = 180^\circ - 70^\circ = 110^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.